A hiperbola kanonikus egyenlete
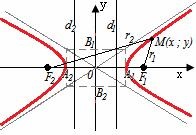
A hiperbola a pontok helyzete, amelyek mindegyikéhez a távolságok közötti különbség modulja két ponttól F1, F2 (foci) egy állandó érték, amely egyenlő a 2a értékkel.
- asymptote
- excentricitás (c> a). Az aszimptoták közötti szög megoldásának nagyságrendjével számszerűsíthető.
r1 = ± (# 949; x-a), r1 = ± (# 949; x + a), - a gyújtó sugár (a felső jel megfelel a jobbnak, az alsó a bal oldali ágnak)
- iskola-igazgatónő
A képzeletbeli tengely geometriai jelentését ábrázolja szaggatott vonallal (az aszimptoták közötti távolság).
A hiperbola kanonikus egyenlete (a koordináta tengelyei egybeesnek a hiperbola tengelyével):
Egy equilaterális hiperbola tulajdonságai
A képzeletbeli 2b tengely nagyobb, kisebb vagy egyenlő lehet a 2a valós tengelyével. Ha a valós és a képzeletbeli tengelyek egyenlők (a = b), akkor a hiperbolt egyenlő oldalúnak (vagy egyenlőnek) nevezzük. Egy equilaterális hiperbola excentricitása sqrt (2).
Az egyenlő oldalú hiperbola aszimptotjai egymásra merőlegesek.
Konjugált hiperbolák
Két hiperbolátot konjugáltnak neveznek, ha közös központjuk és közös tengelyük van, de egyikük tényleges tengelye a másik képzeletbeli tengelye. A konjugált hiperbolák közös aszimptotákkal rendelkeznek.
Egy hiperbola konjugátum egyenlõdése egy adott halmazhoz:
Ennek a hiperbola tényleges tengelye megegyezik a másik képzeletbeli tengelyével.
Lásd a második rend görbéit (Ellipszis, Kör, Hyperbola, Parabola).