Építése a stabilitási régiót
Előadás 15. építése stabilitási régiót. A megosztás fogalma D-
Építése a stabilitás és a D- partíció használt befolyásának tanulmányozására rendszer paraméterek értékeit stabilitását és minőségét.
Stabilitás régió a tér a rendszer paramétereit (áttételek, a rendszer időállandó és más egységek.) Az úgynevezett egy sor paramétereket, amelyek alapján a rendszer stabil.
A határ a rendszer stabilitását megfelelnek a fenntarthatósági határainak:
- aperiodikus (jelenléte nulla gyökér a karakterisztikus polinom) megszerzésének feltétele nulla konstans a karakterisztikus polinom, egy = 0;
- megfelelő végtelenített gyökér a karakterisztikus polinom kapott állapotban A0 = 0;
- vibrációs (jelenlétében egy pár képzetes gyökerek a karakterisztikus polinom) származó feltételeket Dn-1 = 0 összhangban kritériumnak Hurwitz, d (J w) = 0 összhangban kritériumnak Mikhailova vagy W (j w) = - 1 összhangban Nyquist kritérium.
A gyakorlati haszna van az építőiparban a stabilitási tartomány síkjában a két paraméter közül a beállított rendszer paramétereinek megfelelően a funkciók feladatokat. A fő módszer az építkezés használatával jár fenntarthatósági kritériumok Mihajlov.
0AB koordinátarendszer kerül bevezetésre. ahol a tengelyek letétbe értékek A és B rendszer paramétereit.
Az együtthatók a karakterisztikus polinomja a zárt rendszer
kifejezett értékek ezen paraméterek.
A stabilitás határait téregyenleteket felel szerint a fent felsorolt feltételeknek.
A fő összetettsége az építőiparban a stabilitás tartománya kapcsolódó építési a görbe megfelel a vibrációs stabilitási határt. Szerint Mikhailov kritériuma annak vételi komponensei az egyenletrendszert:
, ahol X és Y jelentése a valós és képzetes része a komplex jellemző d (J w). A megoldás lehetővé teszi, hogy a kívánt paraméteres görbe egyenlete formájában A = A (w), B = B (W). Kivétel ezen frekvencia egyenletek nyerhető a szokásos formában egyenlet B = B (A).
Miután megtalálta a határokat a stabilitási tartomány határozza meg a helyét. A határokat az első és a harmadik típusú lehet tenni közvetlenül alapján a szükséges feltételeket a stabilitást. A fenntarthatóság terén kell történnie a0> 0 és> 0.
Mert rezgési határ tekinthető egy további kritérium. Determináns áll a részleges származékok
Ha D> 0, a mozgás a határ mentén irányába gyakoriságának növelése a stabilitást régió balra. Ha D<0 - справа.
Beépített fenntarthatóság területén elfogadott kiosztani keltetés befelé.
Példaként a stabilitási tartomány építeni a rendszer 88. ábrán bemutatott, a síkban a paraméterek k és T1.
Alkotunk karakterisztikus polinomja
és a jellemző komplex
Mi található a stabilitás határán.
1. A aperiodikus határ: an = k = 0. Stabilitás régió megfelel a k> 0.
2. A határ megfelelő végtelen gyökér: A0 = T1T2 = 0. Ennek eredményeként, az egyenlet t1 = 0 határon. Stabilitás-régió megfelel az T1> 0.
3. A rezgési határ:
Ennek eredményeképpen megkapjuk a paraméteres egyenleteket rezgési határ:
Most megszünteti a kapott frekvencia egyenletek:
A megfelelő görbe egy hiperbola (ábra 111).
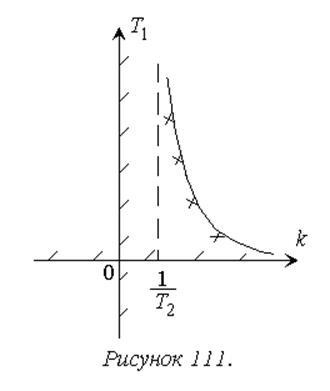
Találunk a helyét a régió stabilitása szempontjából ez a határ tekintettel A = k. B = T1:
Amikor w> 0 növekvő frekvenciák 0 és ∞ megfelel a vibrációs mozgás a határ szerint a paraméteres egyenlet irányába növekvő és csökkenő K T1. ahol D<0, то есть область устойчивости расположена справа.
a w<0 увеличению частоты от - ∞ до 0 соответствует движение по колебательной границе, как следует из параметрических уравнений, в обратном направлении. При этом D>0, azaz a stabilitási tartomány található a jobb oldalon.
D- partíció egy teljes készlet görbék, amelyek megosztják a síkban paramétereket régiók eltérő eloszlása a gyökerek a karakterisztikus polinom D (k).