Aszimptota grafikonjának
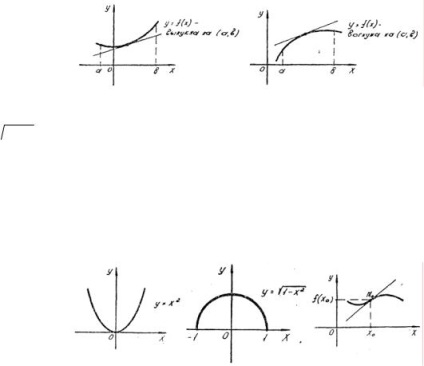
Ütemezése differenciálható függvény úgynevezett konkáv az intervallumot (a, b), ha bármelyik való érintkezési ebben az intervallumban (ábra. 10).
Időzítse egy differenciálható konvex függvény nevezik intervallumban (a, b), ha az kisebb, mint annak bármelyik érintő ebben az intervallumban (ábra. 11).
Mivel a parabola y = x 2 - konkáv függvény teljes tengelye (. A 12. ábrát), és egy félkört y = 1 - x 2 (. 13. ábra) van egy konvex grafikon intervallumon [- 1; 1].
Az M pont 0 (x 0 f (x 0)), ami fekszik a grafikonon, és elválasztjuk a konvex részt generált a konkáv nevezzük inflexiós pont a függvény y = f (x) (ábra. 14).
A dudor (konkáv) funkció "válasz" funkciót vtorayaproizvodnaya = f (x).
Miután az állítás igaz: ha a funkció y = f (x) a második derivált f „” (x) minden pontján az intervallum (a, b), és ha minden pontján az intervallum f „” (x) <0. то график функции в интервале ( a, b ) – выпуклый, если же f ′′ ( x )> 0, akkor a grafikon homorú ebben az intervallumban.
Ábra. 12 ábra. 13 ábra. 14
inflexiós pont kell törekedni azok között a pontokat, ahol a második derivált
Ha a bal az e pont és a jogot a f „” (x) a különböző jeleket, a kapott pont egy inflexiós pontja.
Függvényábrázolási sokkal könnyebb, ha tudod, hogy asymptote.
Aszimptotájának a görbe egy egyenes vonal, amelynek távolsága a pont a görbén nullához közelít végtelen távolságra a származási pont mentén görbe.
Aszimptota lehet függőleges, ferde és vízszintes.
Azt mondják, hogy az egyenes vonal függőleges aszimptotájának a grafikon y = f (x), ha
De ha legalább az egyik ezek a határok nem létezik, vagy egyenlő a végtelenbe, a görbe y = f (x) ferde aszimptotákkal.
Meg kell jegyezni, hogy külön kell vizsgálni az esetek x → + ∞ és x → - ∞. egy speciális esete
ferde aszimptotákkal ha k = 0 és b = lim f (x) egy vízszintes aszimptota. Ezért, az y = b -
Egyenlet vízszintes asymptote.
Tekintsük a ábra grafikonja. 15. A pontok X = 2 x = 4 - pont szélsőértékében a funkciót, a pont x = x 1 - az inflexiós pont. X = X 3 jelentése a különleges pont a funkciót, akkor az f (x) nem folytonos, és az egyenes vonal az x = x 3 függőleges asymptote
A grafikon. Egyenes y = kx + b jelentése aszimptotája a grafikon is, csak ferde, a vonal y = 0 - a vízszintes aszimptotájának a grafikon.
Ha az M pont (x, y) fekszik a grafika és korlátlan elmozdul a származás, mert közel van a következő sorok valamelyike; a távolság M pont (x, y) a aszimptotákkal nullára.
Az általános rendszer a kutatási funkció és a rajzoló
Az általános kutatási funkciója és nyomtatására alkalmas ragaszkodni a következő terv.
Keresse meg a domain a funkció, a funkció pont a szakítás és a folytonosság, hogy megtalálják intervallum (ha lehet) a metszéspontja a grafikon a koordináta-tengely.
Keresse időközönként állandó jel funkció (milyen időközönként kell f (x)> 0 vagy f (x) <0). Решить вопрос о чётности, нечётности, симметрии, периодичности функции.
Ha van egy kis szünetet 2 pont - a második fajta, meg a függőleges asymptote. Megtudja, ha hajlamos és vízszintes aszimptota.
Használata 1 - Oy-származék szélsőérték pont keresés régiót és növekedését és csökkenését a függvény. Keresse meg a szélső értékei a funkciót.
Segítségével 2 - oy származék lelet inflexiós pont régiója konvexitás és konkáv. Szerkesszünk egy grafikont.
Példa: Annak vizsgálatára, az y =