Kombinált ingadozások - automatizált online rendszer kialakulásának adatbázisok
Kombinációs ingadozások, adódó ingadozások kitéve a nem-lineáris rendszer két vagy több harmonikus vibráció különböző frekvenciájú komponenseket. A frekvenciákat a rezgéseket kifejezett összetett összege vagy különbsége minden pár frekvenciák oszcillációk érintő rendszer, illetve alkotóelemei. A legegyszerűbb esetben, amikor két rezgés chastotamiω1 és ω2 a rendszerbe. kénytelen vibrációs spektrum tartalmaz komponensek chastotamiω = mω1 ± nω2. ahol m és n - egész számok.
Hagyja, hogy a nemlineáris eszköz, amelynek jellegzetes van ábrázolva elegendő közelítési képlet
i = αu + βu 2 (1)
összeg két szinuszos feszültségekkel
vagy a következő változás,
Ez azt mutatja, hogy a jelenlegi egy olyan konstans komponenst és hat különböző rezgési frekvencia: ω1. ω2. 2ω1. 2ω2. ω1 -ω2. ω1 + ω2. Mindegyik rezgések lehet izolálni hangolt rezgőkör is. Rezgések frekvencia ω1 -ω2 és ω1 + ω2. előforduló csak a jelenléte a két alkotó u1. u2 mellékelt ingadozások u. Úgy hívják Raman rezgéseket. és azok gyakorisága kombináció frekvenciákat. A frekvencia különbség ω1 -ω2 hívják, és a frekvencia ω1 + ω2 - összesen. A különbség frekvencia van különös jelentősége.
Ha a jellemző sokkal bonyolultabb, mint (1), amelyek bonyolultabb összetett frekvencia típust mω1 ± nω2. ahol m, n - egész számok.
Régen a tudományos és műszaki hatásai
Előfordulás kombinációs rezgések alapját a legtöbb frekvencia konverziós technikák - moduláció. felderítése. megszerzése egy közbülső frekvenciájú. Kombinált ingadozások is előfordulhat lineáris rendszert, ha annak bármely paraméter változik időről időre. Ebben az esetben, még akkor is, amikor arra harmonikus rezgések lépnek az összetett rezgési frekvenciája. megfelel egy lineáris kombinációja a két frekvencia. és működtetjük a frekvencia paraméter változás.
Ha a jellemző sokkal bonyolultabb, mint (1), amelyek bonyolultabb összetett frekvencia típust mω1 ± nω2. ahol m, n - egész számok.
Az úgynevezett módszer befogadására a fül nélküli távíró jeleket. A nemlineáris eszköz ingadozása összeg bemeneti
u = a [1 + f (t)] cosωt,
bol az adó, és fluktuációk
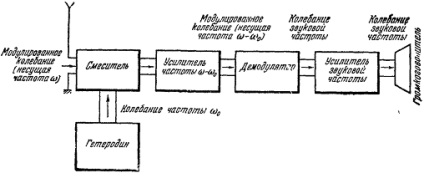
Formation különbség oszcilláció is szolgáló intézkedés egy szuperheterodin vevő, a legelterjedtebb jelenleg típusú rádiók. Ez a bejövő modulált oszcilláció és szinuszos oszcillációs U0 = A0 cosω0 t, által generált az oszcillátor alkalmaznak két elektróda „keveredés” izzó. Ez képezi a swing arányos
Mindkét kifejezés (oszcillációs frekvenciát különbség ω-ωo és az összeg frekvencia ω + ωo) vannak modulálva amplitúdója. modulációs forma megegyezik a bejövő rezgések. A frekvencia a helyi oszcillátor változik kézhezvételét követően az adott állomáson. Vevő beállító gomb módosításokat egyidejűleg a vevőáramkör bemeneti kapacitást kondenzátor (ez hangol frekvencia ω), és a kondenzátor kapacitása oszcillátor (mozgatható kondenzátor lemez mind ültetett egy közös tengelyen). A kontúrok úgy tervezték, hogy a különbség frekvencia forgatásával hangológomb vevő állandó marad. További kiválasztási történhet rezonancia és amplifikáció a különbség fluktuáció és végül annak demoduláció, ami után a demodulált oszcilláció amplifikáljuk és betápláljuk a hangszóró (1. ábra).
A tömbvázlatát szuperheterodin vevő
Amikor a fül ugyanakkor van két szinuszos akusztikus rezgések nagy intenzitású különböző frekvenciájú ω1 és o2 halljuk nemcsak a hangok megfelelő ezeket a frekvenciákat, hanem a további hangok frekvencia ω1 - ω2 és ω1 + ω2. Ezek a kombinációs hangok vannak kialakítva, mivel a nemlinearitás a fülben. Nemlineáris annak a ténynek köszönhető, hogy az elmozdulás a dobhártya a fül (és más) nem szigorúan arányos a nyomás, azaz. E. nem engedelmeskedik Hooke-törvény pontosan.
Az akusztika van egy másik mechanizmus a kombináció hangokat, amelyek teljesen függetlenek a füléhez. Ez okozta nemlineáris a közeg, amelyben a terjedési hang, különösen levegőben. De ez nemlinearitásnak jön szóba, ha a intenzitás jóval magasabb, mint a már jelenleg is érezhető kombináció hangokat, amelyek következtében képződött nemlineáris a fül.
1. Nagy Szovjet Enciklopédia / Ch. Ed. AM Prohorov. Ed. számítanak. N.K.Baybakov, VH Vaszilenko, LM Volodarsky, VV Volsky és mások-M. Szovjet Encyclopedia, 1987
2. "Principles of rezgés elmélet" Migulin VV, Medvegyev VI Mustel ER Parigin VN - M. Nauka 1978.
Ez megköveteli támogatja a belső kereteket.