Integráció tekintetében a Simpson módszer
Legyen n = 2m - páros szám, és yi = f (xi) (i = 0..n) - értékét a függvény y = f (x) egyenlő távolságra lévő egy = x0. x1. x2. ..., xn = b lépése h = (b-a) / n = (b-a) / 2 m. Egy pár szakaszok (3. ábra) görbe y = f (x) helyébe a parabola y = L (X), amelynek együtthatókat úgy választjuk, hogy az áthalad a ponton y0. y1. v2.
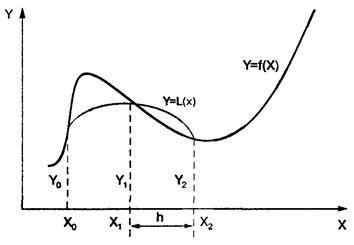
3. ábra Geometriai értelmezése integráció Simpson-féle módszerrel.
A területet a görbe vonalú trapéz határolt felett a parabola, a következő lesz:
Összefoglalva a teljes terület a görbe vonalú trapéz, kapjuk:
Ahol p = 6-p, p = 4. Következésképpen, Simpson képlet numerikus integrációja formájában:
A fennmaradó kifejezés a forma:
A gyakorlatban megbecsülni az abszolút hiba Simpson-féle képlet a következő összefüggések érvényesek:
Ugyanakkor, mint a szabály, hogy túlbecsülni.
2. szabály Runge (n - páros szám) ad finomabb értékelése:
De lehet kapni alacsony becslés, hogy kell tartani.
Formula téglalapok és trapézok ad a pontos értékét az integrál, amikor az integrandust f (x) jelentése a lineáris. mert akkor f „(x) = 0, és a Simpson-féle képlet pontos polinomok fel a harmadik fokozat. t. k. Ebben az esetben, az F (4) = 0.
Ha a függvény az y = f (x) táblázatos és származékai nehéz megtalálni, a feltételezés a hiánya gyors oszcilláló komponensek használhatók közelítő képletek hibák, kifejezve a véges különbségek:
1. Tegyük fel, szeretnénk számítani az integrál precíziós # 949;. A megfelelő képlet a fennmaradó R, H úgy választjuk meg, hogy megfelel a egyenlőtlenség.
2. Dupla Central. (Szabály Runge).
Numerikus megoldása a transzcendentális, és a nemlineáris egyenletek.
Ha egy algebrai vagy transzcendens egyenlet meglehetősen bonyolult, gyökerei viszonylag ritkán lehet találni pontosan. Ezért nagy jelentőségű a közelítő módszereket találni a gyökerei egyenletek és értékeli a pontosságát.
A folyamat a megállapítás a közelítő értékek a gyökerek az egyenlet:
ahol az f (x) van meghatározva, és a folyamatos át néhány véges vagy
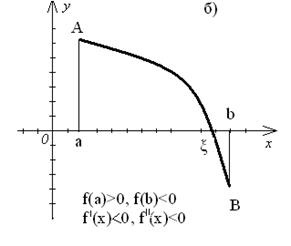
végtelen intervallum bármilyen értéket # 955;, megfordításával az f (x), hogy nulla, vagyis oly módon, hogy az f (# 955;) .. = 0 hívják a gyökér a (1) egyenlet vagy nulla f (x). Külön a gyökerek - ami azt jelenti, hogy megtörje az egész tartományban a megengedett értékek szegmensek, amelyek mindegyike tartalmaz egy gyökér. gyökerek elválasztást lehet tenni két módon - grafikus és analitikai. Grafikus módszer elválasztó gyökerek. a) ábrázoltuk függvény az y = f (x) az egyenlet formájában f (x) = 0. Az értékek a valós gyökereit az egyenleteket abszcisszán metszéspontjai az y = f (x) x-tengely (1. ábra); b) képviseli a (1) egyenlet, mint a # 966; (x) = g (x), és a rajzoló funkciókat y = # 966; (x) és y = g (x). Az értékek a valós gyökereit az egyenlet abszcisszái A metszéspontok a grafikonok funkciók y = # 966; (x) és y = g (x) (2. ábra). A szegmensek, melyek körülveszik csak egy gyökér, könnyen megtalálható. Az analitikai módszer azon alapul, a szétválasztása gyökerei a következő tétel: ha a folyamatos a függvény a végein a szegmens értékek a különböző jelek, azaz a . ezen belül intervallum legalább egy gyökere az egyenlet; ha ez a származéka folyamatos jel belsejében a szegmens. A gyökér az egyetlen. Finomítás gyökerek egy előre meghatározott pontossággal. Azaz szűkülete szegmens lokalizációja a gyökér [a, b]. Tekintsük néhány módszer. felező módszer (kettősség). Hagyja elválasztjuk gyökér és tartozik a szegmensben. Find a középpontját képletű (3. ábra). Ha. majd - a kívánt gyökér. Ha. majd válassza ki a másik fele egy új szegmens vagy root elszigetelten. azaz úgy értékei különböző jelek. Más szóval, ha. akkor a gyökér tartozik a szegmensben. ha - a szegmens. A kapott felére csökken újra osztani találunk. Számoljuk. válassza ki a szegmens, stb Amint azt teljesíteni fogják. majd egy közelítő értéket a gyökér, számított pontossággal. amit megtehetsz. Miután minden egyes iteráció, egy szegmens, amelyen a gyökér a felére csökken, azaz miután n iteráció csökkenti a 2 n-szer. Így, az iterációk számát n ez a módszer függ az előre beállított pontossággal # 949; és az eredeti szegmens hossza, és független a f (x). Ez egy fontos előnye a módszernek a felező képest más módszerekkel. A módszer azonban konvergál lassan megadásakor pontosságú számítás. Legyen a [a, b] az f (x) folytonos, és veszi a végén a szegmens értékeinek különböző jelek, és a származékai a f „(x) és f„(x) fenntart egy állandó jel az intervallum (a, b). Aztán ott vannak a négy esetben a görbe az ív helyét (4. ábra).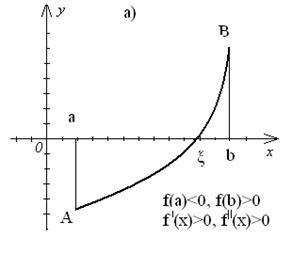
A módszer akkordok a következő közelítő veszi a metszéspont az X tengellyel a vonal (5. ábra), amely összeköti egy pont (a, f (a)) és (b, f (b))
És az egyik ilyen pont van rögzítve - az, amelyre a jelek f (x) és f „(x) azonos.
Fig.5 végéhez rögzített a húrt x = a.
Az egyenlet a húr AB:
A metszéspontja a húrt X-tengellyel (y = 0).
Most, a gyökér a [a, c1]. Cserélje b c1.
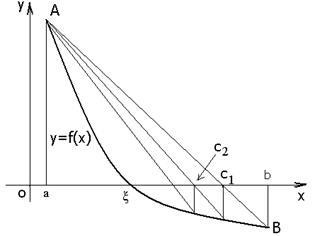
5. ábra. Illusztráció a módszer akkordokat.
Módszer alkalmazásával akkordokat ebben a szegmensben, ezt kapjuk:
Mi továbbra is, stb kapjuk: (2) Feltételek lezárás számítások:
A Hibabecsléseket használhatja általános képlete:
Így, ha f (x) # 8729; f "(x)> 0, a közelítő értéke a gyökér által talált képletű (2), ha f„(x) # 8729; f"(x) <0 (т.е. фиксируется х = b), то по формуле: