Simpson-módszer (parabola), a képlet a becslési hiba, példák, oldatok

A feladat megtalálni a pontos érték a határozott integrál nem mindig a megoldást. Valóban, a primitív az integrandus sok esetben nem ábrázolható formájában elemi funkciót. Ebben az esetben nem tudjuk pontosan kiszámítani a határozott integrál Newton-Leibniz formula. Vannak azonban olyan módszerek numerikus integrálása, amely lehetővé teszi, így az értéke egy határozott integrál a szükséges pontossággal. Az egyik ilyen módszer az a módszer, a Simpson (is ismert parabola).

Oldalnavigáció.

parabola módszer (Simpson) - A módszer, általános képletű, hibabecslés, illusztrálja.

Legyen a függvény y = f (x) folytonos intervallumon [a; b], és azt akarjuk számítani a határozott integrál.

Osszuk az intervallumot [a; b] n elemi időközönként hossza pont. Hagyja, hogy a pont a felezőpontja a szegmensek, ill. Ebben az esetben, az összes „csomópontok” határozzuk meg az egyenletet.

A módszer a parabola.

Minden intervallumban, az integrandus függvény közelíti másodfokú parabola átmegy a pontokat. Innen a neve a módszer - a módszer a parabola.

Ez biztosítja, hogy a közelítő értéket határozott integrálok, hogy ki tudjuk számolni a képlet Newton-Leibniz. Ez a módszer lényege a parabola.

Geometriailag, úgy néz ki, mint ez:

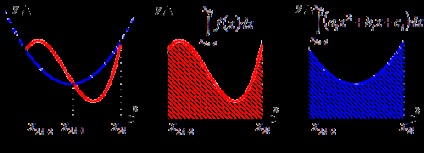
Grafikus ábrázolása a parabola módszer (Simpson).

A piros vonal mutatja grafikon y = f (x). kék vonal a grafikonon a approximáción y = f (x) a másodfokú parabola minden elemi szegmense a partíció.

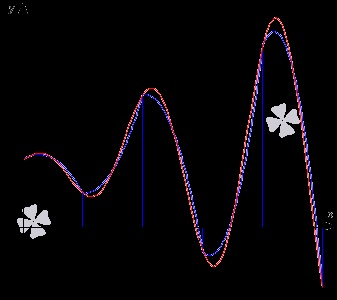
A levezetése a módszer Simpson (parabola).

Azáltal ötödik tulajdonság van egy határozott integrál.

A képlet a parabola módszer (Simpson) azt is meg kell kiszámítani.

Legyen (mi mindig jön rá, ennek megfelelő geometriai transzformációt műszak minden i = 1, 2 N).

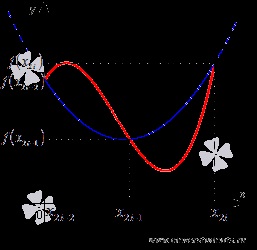
Megmutatjuk, hogy az a pont áthalad csak egy másodfokú parabola. Más szóval, azt mutatják, hogy az együtthatók egyértelműen meghatározni.

Mivel - pont a parabola, igaz, a rendszer egyes egyenletek

A rendszer által rögzített egyenletek egy olyan rendszer, lineáris algebrai egyenletek az ismeretlen változó. A fő meghatározója a mátrix ezen egyenletrendszer a Vandermonde meghatározó, míg a nem nulla elkülönült pontokat. Ez azt jelzi, hogy a rendszer a egyenletek egy egyedi megoldást (leírt a cikkben az oldatot rendszerek lineáris algebrai egyenletek), azaz, az együtthatókat egyértelműen meghatározni, és áthalad a pontokat csak másodfokú parabola.

Most viszont, hogy a meghatározás az integrál.

Ezen egyenletek felhasználásával, hogy végezzen az utolsó átmenet a következő lánc egyenletek:

Így lehetséges a képlet parabolákat módszer:

Képlet módszer Simpson (parabola) formájában van
.

Becslést az abszolút hiba a Simpson.

Az abszolút hiba a módszer a becslések szerint Simpson.

Példák a közelítő kiszámítása határozott integrálok által Simpson (parabola).

Nézzük a használata Simpson módszer (parabola) a közelítő számítást határozott integrálok.

Két típusú munkák jellemzően találtam:

• Az első esetben az szükséges, hogy közelítse a határozott integrál által Simpson-féle képlet egy adott n.
• A második esetben kérte, hogy megtaláljunk egy hozzávetőleges értéke a határozott integrál Simpson (parabola) fel (például, pontossággal, hogy egy ezred).

Van egy logikus kérdést: „A mi pontossággal kell elvégezni a közbenső számítások”?

A válasz egyszerű - a pontosság a közbenső számítások elegendőnek kell lennie. Köztes számítást kell elvégezni pontossággal 3-4 nagyságrenddel nagyobb, mint a sorrendben. Továbbá, a közbenső számítási pontosság függ az n egész szám - a, mint a nagy n. A pontosabb számítások köztes kell végezni.

Számoljuk ki a határozott integrál Simpson, megtörve az intervallum integráció 5 részre.

A feltétel tudjuk, hogy a = 0; b = 5; n = 5; .

Képlet módszer Simpson (parabola) formájában van. Annak érdekében, hogy alkalmazni kell számítani azt a lépést, hogy meghatározza a csomópontok és kiszámítja a megfelelő értékeket a integrandus.

Intermedier számításokat végeznek pontossággal négy decimális (kerekítve az ötödik jel).

Tehát számítani lépés.

Azt viszont, hogy a csomópontok és a függvény értékei bennük:

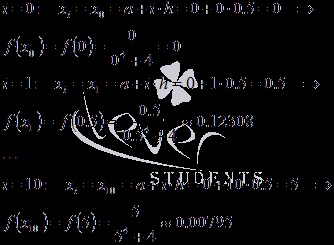
Az érthetőség és kényelem, az eredményeket foglalja össze a táblázatban:

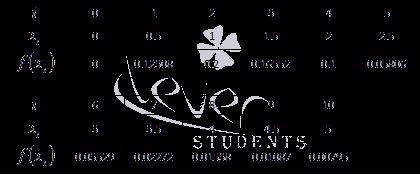
Behelyettesítve ezeket az eredményeket a Eq parabola módszer:

Mi kifejezetten vette a határozott integrál, ami lehet kiszámítani Newton-Leibniz formula összehasonlítani az eredményeket.

Az eredmények összhangban vannak két tizedesjegy pontossággal.

Számítsuk ki a határozott integrál Simpson módszerrel pontossággal 0,001.

Ebben a példában, a = 0 ..

Az első dolog, akkor meg kell állapítanunk n. Ehhez viszont az egyenlőtlenség becslésére abszolút hiba a Simpson. Azt mondhatjuk, hogy ha találunk n. amelyre a következő egyenlőtlenség teljesül, akkor az eljárás felhasználásával számítási a parabola kiindulva szerves abszolút hiba nem haladja meg a 0,001. Az utolsó egyenlőtlenség átírható.

Engedje meg, hogy mi a legnagyobb érték a negyedik modul megkapja a származékot az integrandus intervallumban az integráció.

Tartományban a függvény az intervallum, és az intervallum integráció magában szélsőérték pont, de.

Mi helyettesíti az értéket a egyenlőtlenség és megoldani:

Mivel n egy természetes szám (azonos szegmensek száma, amelybe az intervallum az integráció), lehetőség van arra, hogy n = 10, 11, 12, ... Annak érdekében, hogy ne szükségtelen számításokat, hogy n = 10.

Most, mi jár, mint az előző példában. A kerekítési közbenső számítások kerül sor a hatodik sorrendben.

Keresse meg a csomópontok és az értékeket a integrandust bennük:

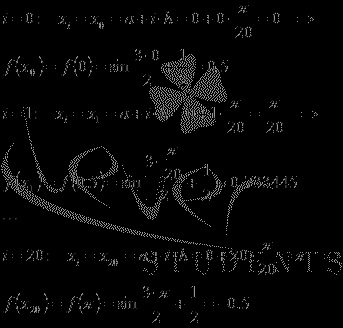
számítási eredményeket kombináljuk a következő táblázatban:

Behelyettesítve értékeket a képlet parabola módszer:

Így szerint a módszer Simpson nyert szerves értéket megközelítő belül 0,001.

Valójában kiszámítása az eredeti szerves Newton-Leibniz formula, megkapjuk

Ez sok esetben nehéz. Meg tudod csinálni nélküle, egy olyan alternatív megközelítés, hogy a használata a parabola módszerrel. Ennek lényegét ismertetjük a trapéz módszer. így nem kell megismételni.

Mi az alkalmazott módszer a numerikus integráció?

A pontosság Simpson (parabola) nagyobb pontosságot a trapezoid módszer és téglalapok egy adott n (ez nyilvánvaló az értékelésből az abszolút hiba), így annak használata előnyös.

Emlékeztetni kell arra, milyen hatással van a számítógépes hibák az eredményt nagy n. amely késlelteti a közelítő értéke pontos.