Összes cenzúrázott minták
Emlékezzünk, hogy abban az esetben, cenzúrázza függő változó yt helyett az értékeit a fenti (vagy alatt) egy bizonyos szintet, ez a szint tekinthető önmagában.
Például, ha a kereslet meghaladja a kínálatot jegyek, a kereslet szintje az elfogadott több eladott jegyek (cenzúrázza felülről). Ebben az esetben, a megoszlása a valószínűségi változó lehet leírni, mint egy kombinációja diszkrét és folytonos eloszlások (lásd. Ábra. 10.9).
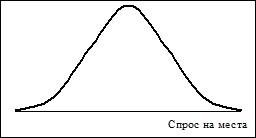
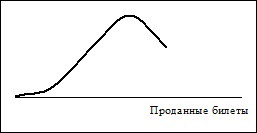
Ábra. 10.9. Distribution cenzúrázott „felülről”
Megközelítések a tanulmány a cenzúrázott és csonkított minták nagyon hasonló. Azt is, hogy általában feltételezik, hogy a véletlen változó y normális eloszlású.
Megmutatjuk, hogyan lehet megváltoztatni a véletlen várható értéke és szórása y változó. Ha a minta értékeinek cenzúrázzák az alábbiakban.
Bemutatjuk az új véletlen változó Y *. oly módon, hogy
ahol b - cenzúrázza pont.
N [M, S 2], a várható értéke és szórása a véletlenszerű változó y cenzúrázott rendre *
Leírására változó függőség cenzúrázott yt származó befolyásoló tényezők gyakran használják az úgynevezett tobit -modell.
Tobit- modell feltételezi, hogy cenzúrázott variábilis YT ismertetjük a következő egyenlet:
ahol yt - a megfigyelt értékek a függő változó (pl tényleges vagy üdülési kiadások külföldön, vagy 0); xt - vektor független változók, amelyek befolyásolják a függő változó yt. egy - paraméter vektor; et - modell hiba.
Tól (10,159), hogy a feltételes várható a változó yt XT tényező meghatározása az
Az elvárás alapú cenzúrája yt (.. M e M [yt árakon]) a pont cenzúrázza b = 0, a következőképpen határozzuk meg (lásd expresszióját (10,154).)
Összhangban expressziós (10,160) tűrési tényező hatása az elvárás xt yt változó (kivéve cenzúrája) definiált
Összhangban expressziós (10,161) marginális hatások xt tényezők az elvárás tekintve változó yt cenzúrázza lehet az alábbi képlettel ábrázolható:
Megjegyezzük, hogy tobit-modell feltételezi, hogy a változás a tényezők xt vezet az a tény, hogy a valószínűsége P (yt> 0), és a várható M (yt | yt> 0) biztos, hogy változtatni ugyanabba az irányba. Valóban, szerint (10,156), annak a valószínűsége, hogy a youtube> 0 jelentése a
Ennek megfelelően marginális hatás xt tényezők a valószínűsége P (yt> 0) lehet az alábbi képlettel ábrázolható:
Ha ai együttható pozitív, akkor szerint a egyenletek (10,164) és (10,166) növekvő hit faktor (i = 1,2 n; t = 1,2 T ..) növekszik, ahogy az elvárás M (yt | yt> 0), vagy és a valószínűsége P (yt> 0), és fordítva, egy negatív növekedési faktor ai, hogy elérje ezeket a számokat csökkennek.
Ugyanakkor megjegyezzük, hogy a hatás a párhuzamosan növelte várakozás és bizonyos valószínűséggel egyre xi független tényező a gyakorlatban nem lehet a helyzet. Különösen, amint azt a Schmidt és Fin (Fin és Schmidt, 1984), a független változó xi. növeli a valószínűségét, cenzúrázatlan megfigyelések (P (yt> 0)), nem mindig növekszik, és a várakozás egy változó (M (yt | yt> 0)). Példaként idézik a veszteség tüzek épületek. A tűzveszély egy régi épület felett, így ¶P (yt> 0) / ¶hit> 0 (hit - életkor t-edik az épület), de a régi épület olcsóbb, majd tüzet hoz kevesebb veszteséget így. . ¶M f (yt | yt> 0) / ¶hit <0. Таким образом, в данной задаче предполагается, что коэффициент ai при факторе “возраст здания” имеет разные знаки в функциях вероятности и математического ожидания. В рамках tobit -модели это учесть невозможно.
Ahhoz, hogy leírja azt a folyamatot, amelynek során a feltételezés az azonos jellegű, a marginális hatása a valószínűség és a matematikai elvárás nem teljesül, akkor már felajánlott egy általános modellt, amely kombinációja egydimenziós modell probit és csonkított regresszió (cenzúrázva értékeket a függő változó).
Valószínűsége alapján határozzuk meg probit -modell cenzúrázott (vagy cenzúrázott) adott elrendezése mellett a megfigyelés xt tényezők.
ahol F (g ¢ xt) - a kumulatív normális eloszlás, ahol meghatározzuk annak valószínűségét cenzúrázott megfigyelések; g - a vektor a modell paramétereinek, ZT - egy indikátor változót, amely veszi a értéke 1 cenzúrázatlan megfigyelések és 0 - a cenzúrázzák.
Ezután alapján csonka regressziós modellek határozzák meg a várható cenzúrázatlan észrevételeit. Összhangban expressziós (10.150) elvárás cenzúrázatlan változó lehet az alábbi képlettel ábrázolható: