Az előrejelzések ívelt vonalak és felületek
Lapos görbe vonal hívják vonal, amelynek minden pontja ugyanabban a síkban. Ellenkező esetben görbe nevezett térbeli (spirális vonal, a vonal metszéspontjában két felület, amelyek közül legalább az egyik egy görbe felület).
Jogos vonalak által leírt egyenletek és algebrai osztva a második és magasabb rendű és transzcendens le a trigonometrikus függvények. Az, hogy a görbe vonal - ez a foka az egyenletet, vagy több egyenes vonal metszéspontjai vonal (sík görbék), vagy a pontok száma keresztezi a sík (térbeli vonal). Curves másodrendű néha nevezik conics.
Torispherical vonalak (vagy kontúrok) nevezzük kompozit görbék, ívek egymás után határozzuk pár bypass pontot. Ha az ízületek lehet építeni egy közös érintője, a bypass nevezik sima. A kör alakú vonalak nevezik vonalak, az építési amely képes szállítani egy iránytű (ovális, tojásdad, Curl et al.).
Egyenes nevezett sík görbék jogos vonalat, amikor ábrázoljuk, hogy használati szokások (ellipszis, parabola, hiperbola, stb.)
Ciklikus görbe vonalak - vonalak megismételjük a folyamat kialakulásának (ciklois, epiciklois és hipociklois al.).
Sima görbék állnak a közös pontokat.
Közös pont a görbe - ez az a pont, ahol meg lehet építeni egyetlen érintő a görbe. Ha a görbe tartalmaz egy speciális pont, a vonal az úgynevezett nem sima.
Ekvidisztáns és ekvitangentnye vonal - egy vonal egyenlő távolságra egy bizonyos vonalat a görbe és megismétli az alakját.
Közelíteni vonal - vonal mintegy helyébe
Más kényelmesebb telek vonalak (például ellipszis néha helyébe egy ovális).
Lapos tér görbék
A leggyakoribb módszer használt egyenes vonalú görbéket, amely lehet sík, és a térbeli. Ezek közé tartozik egy ellipszis, parabola, hiperbola, evolvens, cikloid, spirális vonal, és mások, melyek példái az 1. ábrán megalkotásának eljárásai egyenes görbék általában úgy során technikai
Evolvens - röppálya érintési pont, tekercsek nem csúszik a kör. Néha tévesen nevezik leolvasó kört.
Szinuszos - egy görbe által leírt egyenlettel y = sin x.
Hiperbola - a pontok helye, ahol a különbség távolság két pont az úgynevezett gócok állandó.
Helix - pályája mentén mozgó egy alkotója a henger, kúp vagy tórusz, míg a generátor maga egyenletesen forog a tengelye körül a nevezett felületek.
Ellipse - a pontok helye, amelynek összege a távolságot két pont hívott gócok állandó.
Parabola - a pontok helye egyenlő távolságra egy pont, úgynevezett fókusz, és egy egyenes vonal, az úgynevezett direktrix.
Ciklois - pályája egy kör, amely gurul csúszás nélkül az egyenes. Amikor létrehozunk egy hipociklois epi- és gurul a kör kerülete.
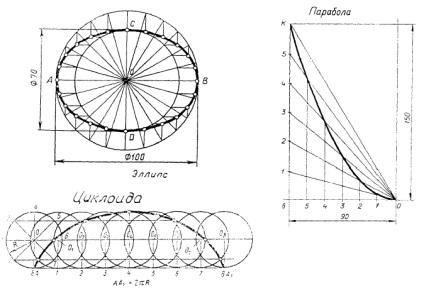
1. ábra - Az egyenes görbék
Az építés egy görbe vonal előrejelzések
Vetítővonal görbe a következő tulajdonságokkal:
Általában, a vetítési vonal görbe görbe vonal;
Ha a pont tartozik a vonal görbe, a vetítés
Ők tartoznak az azonos nevű kivetített görbe
Az érintőleges görbe vonal tervezett érintő
kivetített görbe vonal.
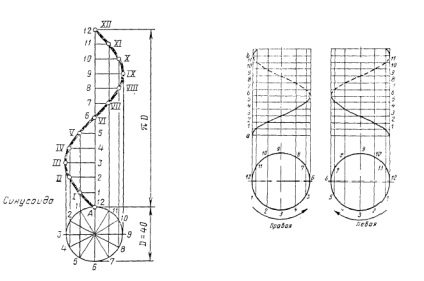
1. példa. Construct vetítési jobb hengeres csavarvonal áthaladó henger.
2. ábra - az 1. példában.
MEGOLDÁS. Megtaláljuk a pont /. Mivel pont /. ossza el a henger kerületének 12 alap részeket. A H magassága a henger osztva 12 rész, kiindulva az A pont //. A kereszteződésekben a függőleges és vízszintes vonalak a hasonló spirál megtalálni a pontokat, amelyek simán kapcsolják össze (2. ábra).
Általános információk a felületek
Surface - ez a locus a sor halad az űrben szerint egyes törvények. Ezt a vonalat nevezzük a képet. Lehet egyenes, akkor képződik a felület osztályába tartoznak a vonal. Ha a kép - egy görbe felület akkor tekinthető nem zárható. A vonal mentén, amely azt hívják az útmutató. Ennek az utolsó pálya felülete néha használják.
Meghatározója a felület azoknak a feltételeknek a meghatározása felület a térben.
A felület akkor tekinthető egy adott, ha van lehetőség, hogy egy kép kiálló. Az ugyanazon a felületen kialakítható különböző vonalak a mozgás. Például, egy gömb van kialakítva forgatásával egy kört az átmérője.
A megfontolt felületi alábbiakban a következőképpen osztályozzák.
I. forgás uralkodott felületeken.
II. forgásfelület nem zárható.
A tórusz (kör alakú, parabolikus, elliptikus).
Ellipsoid (lapított és tömörített).
Rotációs felszíni általános formája.
III. Felületeket sík párhuzamosság.
IV. Felületek Ismételt keretben.
Zárható forgásfelületté
Minden felület ezen osztály által kialakított forgó egyenes körül a többi egyenes. Két vonal lehet elfoglalni egymáshoz képest három különböző pozíciókban. Mindegyikük saját forgási felület.
1
.Cone kialakítva forgatásával egy egyenes vonal metsző OD körülötte Z tengely (3A.). A koordináta síkok XOZ és Yoz tagolt metsző kúp Direct OD, OE, OK és az OF; sík XOZ ad metszeti O pont; síkra. párhuzamos XOY, metszi a kerület menti (DFEK).
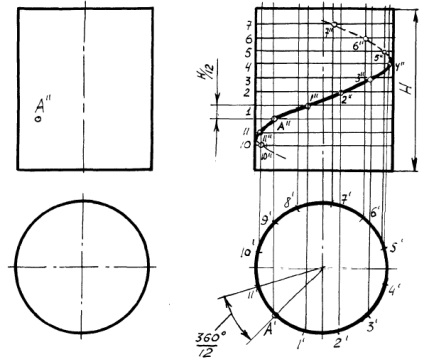
A konstrukció pontok tartozó felület görbe, amely a felületén kiemelkedések vonal feküdt a felszínen.
Cone részt vesz a kialakulását az antenna alakja tartalmazza a sugárzási karakterisztikát, a felület helyzetét a tárgy a térben, az antenna és a takarmány, hangszóró kúp, az üreg reflektor rádióhullámok, elektroncsövek és vákuum csövek, rost, vákuum berendezések alkatrészek és így tovább.
2
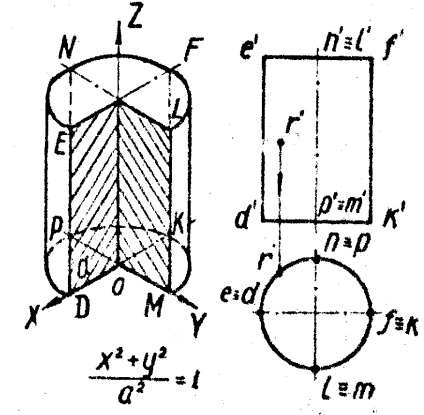
.A kialakított henger körüli forgása párhuzamos egyenes hozzá ED Z tengely (ábra. 3b, c)
XOZ és Yoz síkok mentén metszik párhuzamos egyenes az ED, FK, NP, LM, és a XOY sík, és vele párhuzamosan - körökkel DPKM és (ENFL).
A henger használt kialakulását alakos hullámvezetők antennák csappantyú eszközök, lézer tükrök, házak érzékelők és így tovább.
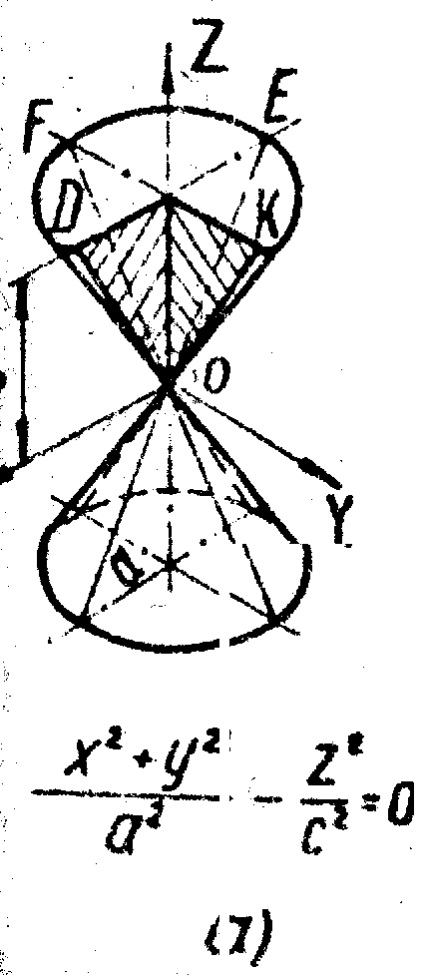
3.Odnopolostny hiperboloid alkotnak körüli elforgatás a vonal ED keresztezzük vele Z tengely (ábra. 4).
Sík XOZ és Yoz át a hiperbola FK, LM, PQ és RS, valamint XOY sík és vele párhuzamosan - a körök (GU, FPLR és KQMS). Upon forgatóképesség D és E pontokat a nyúlványok D és E jelentése kerülete mentén mozgatjuk, és a nyúlványok a D és E - egyenes vonal mentén párhuzamos az X tengellyel a ponton egy egyenes U DE, legközelebb elhelyezkedő forgástengely, kört ír le UU1 legkisebb átmérőjű. Ez a kör az úgynevezett torok felszínén. Rays kiálló bármilyen felületen, kapcsolódik, hogy a pontokat alkotó szintvonal. Megfelelő a vetületét ezen a vonalon nevezzük vázlat felületre.
Kereseti hiperboloid imeyutnekotorye rádió tornyok. Ez alkotja továbbá alakja vibráló adagolók használják az ipari automatizálás, a bütykös érintkezők csatlakozók, és így tovább.
Ahhoz, hogy ez az osztály tartoznak elsősorban felület által alkotott forgó görbével másodrendű.
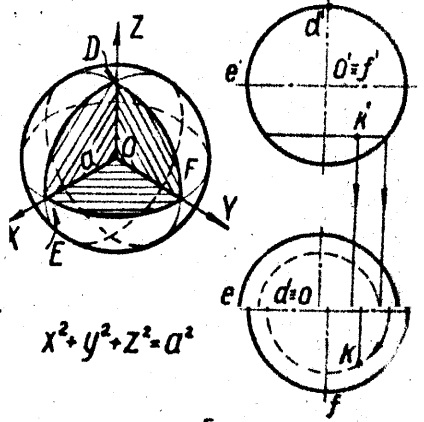
1. Gömb forgás egy kört formálnak annak átmérője (ábra. 5)
Bármilyen sík metszi a gömböt kerülete mentén. Esszé az első vetítés a gömb az úgynevezett fő meridián. vázlatot a vízszintes vetülete - az Egyenlítő. Az előrejelzések pont K feküdt a felszínen egy gömb, kör tartozik, tervezettnél vízszintes végzett a gömböt.
Scope meghatározza alakú mintázat az antennát, orrkúp és az antenna radiátor, fej mikrofon, relékontaktusok, és így tovább. A gömb egy felület helyzetének az objektum a térben.
2.Krugovoy tórusz kialakított forgó kör tengely körül síkjában fekvő kör és átmérője lény. Fentiek értelmében lehet tekinteni, mint egy speciális esete a tórusz. Megkülönböztetni tórusz gyűrű. amikor a forgástengely nem metszi a kerület, és a tórusz-hordó.
A rádió is használják parabolikus és elliptikus tórusz.
Parabola tórusz forma parabola körüli forgása egyenes síkjában fekvő parabola és nem gyújtópontjának tengely.
Az elliptikus tórusz kialakított forgó ellipszis köré egy egyenes vonal síkjában fekvő ellipszis, és amely a tengelye körül.
Tore felületek van antenna minta, a felület helyzetét a tárgy a térben, antennák és radomok, hullámvezetők, rezonátorok, a hangszórók és így tovább.
Ellipszoid forgó ellipszis körüli kisebb vagy bolshoyosi. Az első esetben, egy tömörített (6a ábra.), És a második - egy hosszúkás ellipszoid forgástest (6. ábra, b.).
Sík XOZ és Yoz át őket végig ellipszis DE és EF és XOY sík - a DF kerülete.
ellipszoid alakú tükrös lézerek és antennák, antenna radiátorok, a felület helyzetét, és így tovább.
Két-sheeted hiperboloid formában a hiperbola DE forgási tengelye körül tényleges FF1 (ábra. 7).
Sík XOZ és Yoz át a túlzó DE és KE; XOY sík ad metszeti képzeletbeli pont O.
Ez az alak a tükör antennák, a felület helyzetét a tárgy térben és így tovább.
5.Paraboloid alkotnak parabola OD körüli elforgatás gyújtópontjának tengelye (ábra. 8).
Mirror antennák és lézerek gyakran termelnek parabola.
6.Poverhnost általános formája által képezett forgástest forgatásával egy tetszőleges görbét.
Felületeket sík párhuzamosság.
Minden felület ennek az osztálynak - uralkodott.
1.Tsilindroid alkotnak egy mozgó vonal a két ívelt vezető, amikor a generátor párhuzamos marad az előre meghatározott síkra. hengerszerű valamilyen formában a háromdimenziós grafika alkalmazott elmélet az optimális irányítás és eltolódások.
2.Konoid alkotnak egy mozgó vonal egy ívelt vonal és egyenes vonal, amikor a generátor párhuzamos marad az előre meghatározott síkra. Egy különleges eset kúpszelet egyenes csavarfelület által alkotott egyenes mentén történő mozgása spirális vonal és a tengelye körül, amikor a generátor párhuzamos marad az előre meghatározott síkra.
3.Giperbolichesky paraboloid vagy ferde síkban egy vonalban mozgását két kitérő egyenes párhuzamos maradjon, amikor alkotó sík. A kapott felület egy nyereg alakú (ábra. 9).
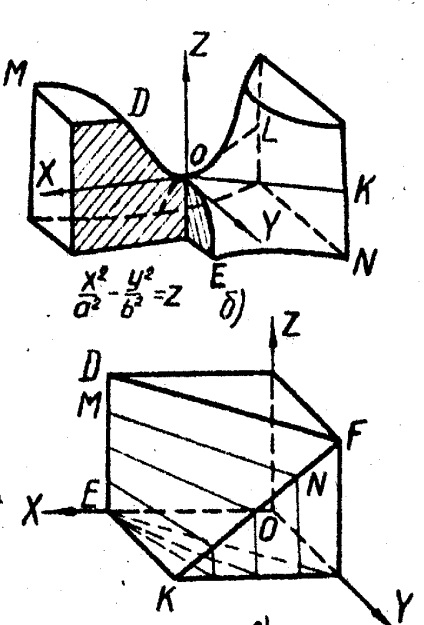
Sík XOZ és Yoz metszik ez a felület mentén, parabola OD és OE; párhuzamos síkban XOZ és Yoz, is ad a parabola keresztmetszetben; XOZ metszi a két egymást metsző vonal ol és OK, és a sík párhuzamos XOZ, - a hiperbolák (EN és DM).
Felületek Ismételt keretben.
Ezek közé tartozik felülete, a kialakulását, amely nem függ egy adott geometriai törvényt. Ezek a felületek határozzák meg a keretet - a család sor, hozzájuk tartozó, és ezzel párhuzamosan a koordináta síkok (10. ábra).
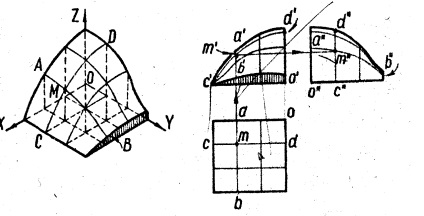
Ábra. A 10. ábra egy térbeli grafikon alkalmazott rádiótechnika. A felület által meghatározott görbék, az egyik családja, amelyek (CD) síkjával párhuzamos XOZ és a másik (AB) - Yoz síkban. Az M pont úgy definiáljuk, mint egy felszíni metszéspontja a görbék AB és CD.
Az elektronika és az automatizálás fordulnak elő négyzetes felülete általános formája elliptikus kúp és a henger, parabolikus és hiperbolikus hengerek és így tovább.
Listája irodalomból.
Anisimov IK összefoglalói előadások ábrázoló geometria. - R. 1970.
Frolov SA Ábrázoló geometria: a tankönyv középiskolák. - M. Engineering 1983.