Menetrend jellemzői ábrázolástól leckét algebra 10 osztály bemutatása
Srácok, mi építettünk sok grafikonok funkciók, mint például egy parabola, hiperbola, grafikonok trigonometrikus függvények, és mások. Emlékezzünk arra, hogyan csináltuk. Úgy döntünk, egy pont az x tengelyen és számított értékei a koordinátáit a funkciók és zökkenőmentesen csatlakozni a koordinátákat a koordináta síkon. Vagyis, mi függvényében pontról pontra. Az építőiparban a sok grafikonok, a lényeg kell választani szándékosan. Most nézzük összefoglalja a tudás és a levelet az általános építési szabályokat grafikonok a funkciók.
Mi a grafikon?
A grafikon - egy sor pontok abszcisszájú azok az értékek, a domain, és az ordináta - függvény értékei y = f (x). Ütemezése bármilyen funkciót pontja alapján. De ha nem tudjuk pontosan, mi lesz a grafikus formában adják, azt a pontot kell választani szándékosan. Srácok, mi a fontos feladatokat látnak?
Idézzük őket:
a) a helyhez kötött és a kritikus pontokat. Ezek a pontok megtanultuk, hogy megtalálják a számítás a szélsőértékében funkciókat. Ez az a pont, ahol a származék vagy nulla, vagy nem létezik.
b) pont szélsőséges. maximális és minimális pontok funkciókat. Point közelében, ami természete határozza meg az egyhangúságot.
c) a menetrend metszéspontja az X-tengely és az Y-tengely. A értékek, amelyeknél a függvény az y = f (x) = 0 - a metszéspont a abszcissza tengelyen. De ha kiszámítjuk f (0) -, hogy ez a metszéspontja az y tengelyen.
g) pontja, a diszkontinuitás. Ezeket a pontokat keresi, nem folytonos függvények.
Szabály ábrázolási funkciók
Srácok, menjünk írja le az alapvető szabályokat építése grafikonok funkciók:
- Ha az y = f (x) folytonos az egész számegyenesen, meg kell találnunk a helyhez kötött és a kritikus pontokat, a szélsőérték pont, monotonitás időközönként, grafika metszéspontja a koordinátarendszer ki néhány ellenőrzési pontokat szükség szerint, amely az A értékét a függvény .
- Ha az y = f (x) nincs definiálva a számegyenesen, meg kell kezdeni megtalálása a domain a funkció, ami azt jelzi, hogy pont a diszkontinuitás.
- Ez akkor hasznos, hogy vizsgálja meg a funkciót a paritás, mivel a grafikus páros vagy páratlan funkciók a szimmetria (relatív az y tengelyhez, illetőleg, vagy relatív a eredetű), és így meg lehet építeni az első ága a grafikon csak akkor, ha x ≥ 0, majd befejezni egy szimmetrikus ága.
- Ha az egyenes y = b horizontális aszimptotája a grafikon a mi funkciót. Aszimptota - ez egy mérföldkő a funkció. Ez olyasmi, hogy törekedni kell a grafikon a pont, de nem éri el ezt az értéket.
- Ha f (x) = $ \ frac $; és ha X = egy nevező eltűnik, és a számláló nem nulla, akkor x = a - egy függőleges aszimptota.
Néhány szabály, hogy egyszerűsítse az építési grafikonok funkciók:
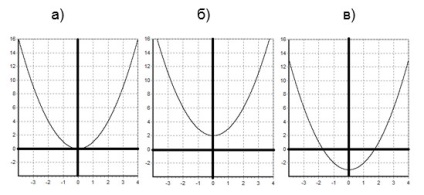
a) A grafikon a függvény y = f (x) + egy nyerik a grafikon y = f (x) (grafikon y = f (x) előre ismert) által párhuzamos átvitel grafikon y = f (x) egy egység felfelé, ha a> 0; és egy egységet lefelé, és ha b 2) y = x 2 + 2, a) y = x 2 - 3.
Grafikonok a funkciók nyert grafikon y = x 2 a párhuzamos átviteli: b) legfeljebb két egység, c) a három egység lefelé.
Táblázatok a mi funkciók:
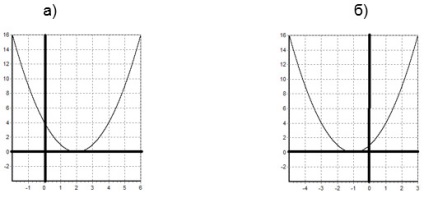
b) A grafikon a függvény y = f (x + a) kapunk a függvény grafikonját y = f (x) (grafikon y = f (x) előre ismert). A párhuzamos fordítás grafikon y = f (x), a bal oldalon és az egységek, ha a> 0, és egy jobb oldali egység, ha a 2. b) y = (x + 1) 2.
Táblázatok a mi funkciók nyerik a grafikon y = x 2 által párhuzamos átvitel: b) a két egység a jobb,) egy egységgel balra.
Táblázatok a mi funkciók:
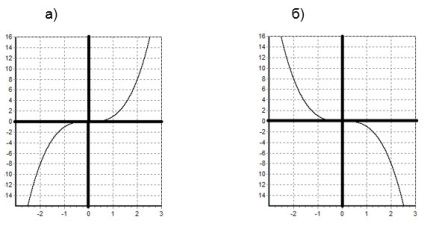
c) Annak érdekében, hogy építeni a grafikon y = f (-x), kialakításához szükséges a grafikon y = f (x), és, hogy az tükrözze a relatív ordináta. A kapott gráf egy grafikon y = f (-x).
Például, konstruálunk két grafikonok: a) y = x 3. b) y = (-x) 3.
Grafikonok a funkciók nyert grafikon y = x 3. keresztül reflexiók koordinálására.
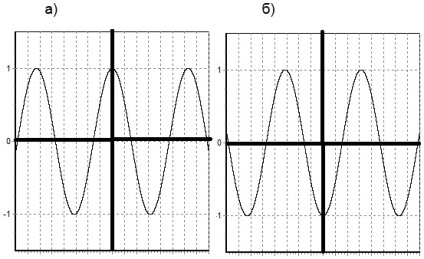
g), hogy plot függvény y = f (x) és, hogy az tükrözze a relatív abszcissza kirajzolásához függvény az y = -f (x).
Például, konstruálunk két grafikonok: a) y = cos (x), b) Y = -cos (x). Grafikonok a funkciók nyert grafikon y = cos (x), keresztül reflexiók abszcisszán.
Srácok, nézzük konstrukció grafikonok a funkciók, a forma, amely nem ismert előre. Fogjuk használni a szabályokat, hogy azonosítottuk az elején.
Példák az építési
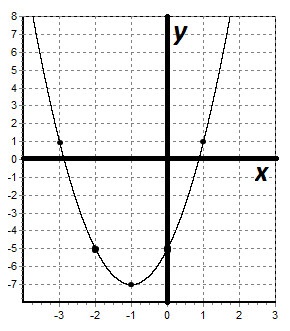
I. Plot funkció: y = 2x 2 + 4x - 5.
megoldás:
1) terület meghatározása: D (y) = (-∞; + ∞).
2) Keresse meg a stacionárius pontok:
y „= 4x + 4
4x + 4 = 0,
x = -1.
3) meghatározza a formáját és jellegét az álló pont monotonitási:
X = -1 - minimális pont. Megtaláljuk a függvény értékét azon a ponton, x = -1
y (-1) = 2 (1) 2 + 4 (-1) - 5 = -7.
Tehát mi funkció csökken az intervallum = (- ∞; -1), X = -1 - minimális pontját a funkció növeli intervallumban (-1; + ∞).
Mi az A értékét a függvény egy pár pontot:
Építünk a függvény grafikonját:
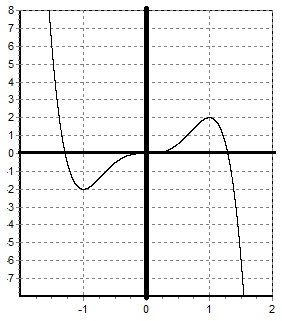
II. Ábrázoljuk a funkció: y = 5x 3 - 3x 5.
megoldás:
1) terület meghatározása: D (y) = (-∞; + ∞).
2) Keresse meg a stacionárius pontok:
y „= 15x 2 - 15x 4
y „= 15x 2 (1 - x 2) = 15x 2 (1 - x) (1 + x),
15x 2 (1 - x) (1 + x) = 0,
X = 0; ± 1.
3) meghatározza a formáját és jellegét az álló pont monotonitási:
X = -1 - minimális pont.
A x = 0 - az inflexiós pont, a funkció ebben a pontban is növeli, de a konkáv változások az ellenkező irányba.
X = 1 - maximális pont.
Azt találjuk, az értéke a függvény a ponton x = -1: y (-1) = 5 (-1) 3 - 3 (-1) 5 = -2.
Azt találjuk, az értéke a függvény a ponton x = 0: y (0) = 5 (0) 3 - 3 (0) 5 = 0.
Azt találjuk, az értéke a függvény a ponton x = 1: y (1) = 5 (1) 3 - 3 (1) 5 = 2
5) tanulmányozza a funkciója a paritás: y (-x) = 5 (-x 3) - 3 (-x 5) = -5x 3 3 + 5 = -y (x)
A definíció szerint egy páratlan funkciót, és a grafikon szimmetrikus az origó.
Ez a függvény a páratlan.
A funkció csökkenti egyenlő intervallum (-∞; -1).
X = -1 - minimális pont. A funkció növeli a (-1, 1).
X = 0 - a inflexiós pontban.
X = 1 - maximális pont. A funkció növeli az (1; + ∞).
Mi az A értékét a függvény egy pár pontot:
Építünk a függvény grafikonját:
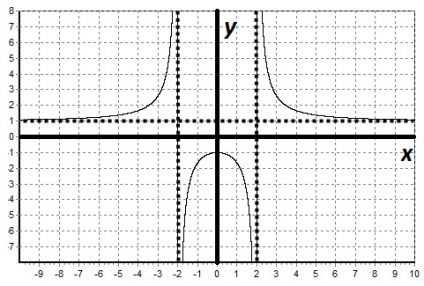
III. Szerkesszünk egy grafikont a funkció: y = $ \ frac $.
megoldás:
1) terület meghatározása: D (y) = (-∞; -2) U (-2; 2) U (2; + ∞).
A definíció szerint egy páros függvény. Ennélfogva, a menetrend funkció szimmetrikus a függőleges tengely az első építeni egy függvény grafikonját az x ≥ 0. 3) Közvetlen X = 2 - függőleges asymptote, hiszen nevezője a függvény ezen a ponton nulla.
Találunk a vízszintes asymptote:
Közvetlen y = 1 - vízszintes asymptote.
4) Keresse meg a helyhez kötött és a kritikus pontokat:
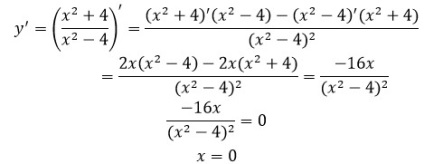
5) meghatározza a formáját és jellegét az álló pont monotonitási pont x = 0 - maximális pont.
Így a funkció még. Ez nő egyenlő intervallum (-∞; 0), X = 0 - maximális pont. A funkció csökkenti a (0; + ∞).
Direct X = 2 - egy függőleges asymptote. Közvetlen y = 1 - vízszintes asymptote.
Mi az A értékét a függvény egy pár pontot:
mert még működnek először megépíteni a grafikon x ≥ 0.
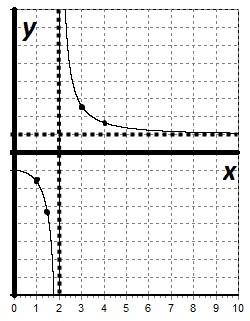
Property még funkcióit tükrözik az ábra a relatív koordináta.
Kihívások a rajzoló funkciók önrendelkezési
1) Ábrázoljuk a funkció: $ y = (-x) ^ 2 + 4x - 7 $.
2) Készítsük el a függvény grafikonját: $ y = x ^ 3 - 3x + 2 $.
3) Döntetlen a függvény grafikonját: $ y = \ frac $.