Nye féle optimalizálási problémák és megoldásuk
Készítmény az optimalizálási probléma „Dana bizonyos függvény f (x1, x2, ..., xn), amely az úgynevezett cél. Meg kell találni maximumot vagy legalább ezt a funkciót hogy bizonyos további korlátozások. Keresési problémák max és min könnyen átalakítható egymással (megszorozzuk az objektív függvény által -1). További korlátozásokat vezetünk általános formában, mint egyfajta nem-lineáris egyenlőtlenségek:
korlátozásokat is be lehet nyújtani formájában egyenlőtlenségek, és a forma egyenletek.
Összesen optimalizálási probléma.
A forma a célfüggvény és korlátok a optimalizálási probléma lehet osztani a következő típusú.
Ha az objektív függvény lineáris és lineáris megkötöttség is, mint például a probléma az úgynevezett lineáris programozási feladat. LP probléma már jól ismert, így van egy linearizáló módszer - nemlineáris konverziós feladatokat egy lineáris formában.
Ha a cél funkció miatt másodfokú formában, akkor a probléma az úgynevezett zadacheykvadratichnogo programozás. Nemlineáris problémák túl gyakran vezet a másodfokú, mert megoldani másodfokú probléma gyakran könnyebb, mint a feladat az általános formában.
Jelenleg továbbra is növekszik köbös programozás elmélet. Egyelőre nem fejlődött ki teljesen.
Ha a korlátozás az objektív függvény hiányzik, vagy van egy egyszerű űrlap xia (korlátozott csupán változó), akkor ez a probléma az úgynevezett korlátozatlan optimalizálás.
Ha a funkció nem lineáris, és vannak korlátai (komplex), akkor a probléma a nemlineáris optimalizálás.
Ha a probléma fennáll paraméterek időtől függően, és jelentősen befolyásolja a döntést, minden egyes alkalommal (összesen van osztva több szakaszban), az optimális megoldást kapunk, és a kapott különböző optimális megoldás az összege hozott döntések minden szakaszában. Megoldási módjait, mint a többlépéses feladatokat olyan módszerekre, amelyek dinamikus programozási elmélet.
A probléma a lineáris programozási (LP), az objektív függvény felírható az összeg a változók bizonyos állandók:
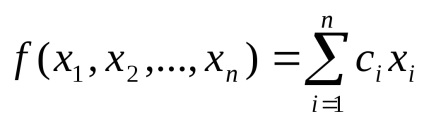
feladat korlátokat lehet bemutatni formájában egyenlőségek és egyenlőtlenségek:

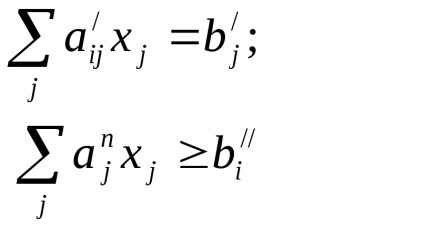
(Korlátozások formájában egyenletek) (egyenlőtlenség korlátok)
Állítsa be a xi az úgynevezett vektor az ismeretlen. Ez a vektor a probléma megoldása ekkor az ismeretlen értéket, ahol az f függvény egy maximális vagy minimális. Az együtthatók ci is képezi egy vektor, amely az úgynevezett vektor források. Elements bi alkotnak vektor úgynevezett vektor készletek. A kényelem, az alkalmazott megoldás csökkenti a problémát az általános kijelentést, hogy egy speciális formanyomtatvány.
Követelmények a szokásos formáját LP probléma:
xi paraméterek nagyobbnak kell lennie, vagy egyenlő nullával (XI 0). Ha van egy ilyen korlátozás, amely lehetővé teszi a negatív érték xi. majd, hogy a változás a változók úgy, hogy az új xi negatív volt.
Egyenlőtlenség korlátok alakítjuk korlátozások formájában egyenletek.
Elements áll a jobb kell, hogy legyen, nem negatív az egyenleteket, azaz bi 0.