11 osztály
Emlékezzünk központi meghatározása - a meghatározása a logaritmus. Ez kapcsolódik a döntést egy exponenciális egyenlet. Az összefüggést egy gyökér, ez az úgynevezett alapú logaritmusa és b:
Logaritmusa b szám az úgynevezett alap, és ez a kitevő, amelyre szeretne építeni egy alap, hogy megkapjuk a számát b.
Emlékezzünk a fő logaritmikus identitását.
Az expressziós (expressziós 1) egy gyökere egyenlet (kifejezés 2). Behelyettesítve a értéke x 1 a kifejezés x expressziós 2, és megkapjuk az alapvető logaritmikus identitás:
Látjuk tehát, hogy minden értéket az adott értéket. Legyen x B (), egy pillanatra, és így megkapjuk a logaritmikus függvény:
Idézzük alaptulajdonságait A logaritmus függvény.
Ismét, figyeljen ide, hogy van. Hogy. A logaritmus lehet szigorúan pozitív kifejezést a logaritmus alapja.
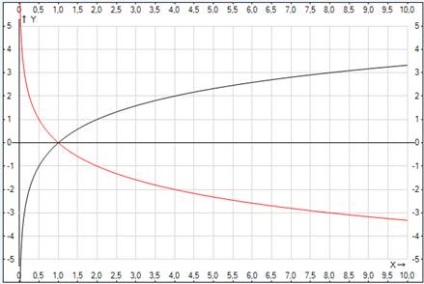
Ábra. 1. A grafikon a logaritmikus függvény különböző okok
Ütemezése, amikor a funkció ábrázolt fekete. Ábra. 1. Ha az argumentum nőtt nulláról a végtelenségig, a funkció növeli mínusz plusz végtelenig.
A grafikon azt mutatja, függvényt, piros. Ábra. 1.
A tulajdonságai ezt a funkciót:
Monoton függvény egész tartományban. Amikor monoton (szigorúan) növekszik, a nagyobb érték az érvelés megegyezik egy nagyobb értéket a függvény. Amikor monoton (szigorúan) csökken, a nagyobb értéke az érv megfelel a minimális érték a funkciót.
Az ingatlan a logaritmikus függvény a legfontosabb, hogy oldja a különböző logaritmikus egyenletek.
Tekintsünk egy egyszerű logaritmikus egyenlet, az összes többi logaritmikus egyenletek, mint általában, csökkennek ilyen formában.
Mivel az alap logaritmus vannak a logaritmus maguk egyenlő és funkciók alapján logaritmus, de nem szabad elveszíteni a domain. A logaritmus csak pozitív szám, van:
Azt találtuk, hogy a f és g függvények egyenlő, így elég, hogy válasszon bármilyen egyenlőtlenség ahhoz, hogy a DHS.
Így van egy vegyes rendszer, amelyben van egy egyenlet és egyenlőtlenség:
Egyenlőtlenség, mint általában, úgy, hogy nem feltétlenül elég ahhoz, hogy megoldja az egyenletet, és találtam helyettesítő gyökerei az egyenlőtlenségek, így érvényesíteni.
Megfogalmazzuk eljárás megoldása egyszerű logaritmikus egyenletek:
Kiegyenlíti a bázis logaritmus;
Egyenlővé logaritmusát funkció;
Tekintsük néhány példát.
1. példa - az egyenlet megoldásához:
logaritmusok bázis kezdetben egyenlő, azt a jogot, hogy egyenlőségjelet tesznek a logaritmusát kifejezés, ne feledkezzünk meg a DHS döntünk, az első log termelni egyenlőtlenséget:
Találunk a gyökér és helyettesítsük be az egyenlőtlenséget:
2. példa -, hogy megoldja a következő egyenletet:
Ez az egyenlet annyiban különbözik az előzőtől, hogy a bázis logaritmusainak kevesebb mint egy, de ez nem befolyásolja a döntést:
logaritmusok bázis kezdetben egyenlő, azt a jogot, hogy egyenlőségjelet tesznek a logaritmusát kifejezés, ne feledkezzünk meg a DHS, úgy dönt, hogy készítsen az egyenlőtlenség a második logaritmus:
Találunk a gyökér és helyettesítsük be az egyenlőtlenséget:
Kapott hibás egyenlőtlenség, akkor megtalálta a gyökér nem felel DHS.
3. példa -, hogy megoldja a következő egyenletet:
logaritmusok bázis kezdetben egyenlő, azt a jogot, hogy egyenlőségjelet tesznek a logaritmusát kifejezés, ne feledkezzünk meg a DHS, úgy dönt, hogy készítsen az egyenlőtlenség a második logaritmus:
Találunk a gyökér és helyettesítsük be az egyenlőtlenséget:
Nyilvánvaló, hogy csak az első gyökér megfelel DHS.
Tehát elkezdték felfedezni egy fontos témában - a döntés logaritmikus egyenletek. Megvizsgáltuk a legegyszerűbb módja egyenletek megoldására és néhány példát annak alkalmazását.