Hasse-diagram
Hasse-diagram - véli diagramok. használni, hogy képviselje a véges rendezett halmaz részben a minta tranzitív annak csökkentését. Pontosabban, egy részben rendezett halmaz (S. ≤) grafikon minden elem, mint egy csúcs S egy sík, vagy görbe szegmenseket és felfelé terjedő elem elem x y. ha x ≤ y és z nem létezik elem. amelyekre x ≤ z ≤ y. Ezeket a görbéket átfedés, de nem mennek át a tetején, ha csak azok nem a vége a sorokat. Egy ilyen diagram jelzett csúcsok egyedileg meghatározó részleges sorrendben.
Először rendszeresen le ez a fajta megjelenítés Birkhoff 1948 [1]. ez adott nevet a megtiszteltetés, hogy az ilyen diagramok Helmut Hasse. de az ilyen számok találhatók korábbi munkák, például a tankönyv francia matematikus, Henri Vogt (it. Henri Vogt) 1895 kiadás. [2]
Bár Hasse-diagram egyszerű és intuitív módon tiszta eszközökkel való működésre véges részben rendezett halmaz. nehéz felhívni a „jó”, hogy kényelmes vizuális érzékelés a diagram elég triviális készletek miatt a nagy számú lehetséges opciókat kijelzőn. Egy egyszerű módszer állítólag kezdeni a minimális elemeket, és felhívni a felettük lévő elemek sorba gyakran ad rossz eredmények - a szimmetria és a belső szerkezet könnyű elveszíteni.
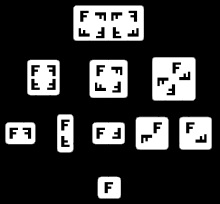
Például, a Boole-készlet négy elem, szabályos működése ⊆ befogadás lehet képviseli a négy alább említett diagramok (mindegyik alcsoportja van látva egy binárisan kódolt címkét, amely azt mutatja, a megfelelő elemet tartalmaz egy részhalmaza - 1, vagy sem - 0):
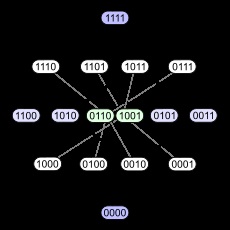
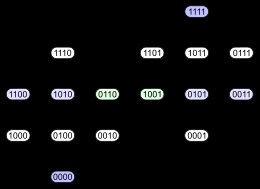
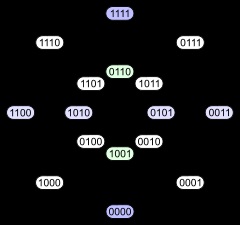
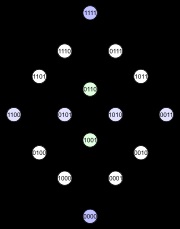
Az első diagram mutatja a szerkezet szintek. A második diagram ugyanolyan szerkezetű rétegek, de van néhány bordája hosszúkás hangsúlyozni, hogy a négydimenziós kocka a szakszervezet két háromdimenziós. A harmadik ábra néhány belső szimmetriát. A negyedik diagram a csúcsok vannak elrendezve, mint egy mátrix 4 × 4.
Hasse-diagram alcsoport rácsos diédercsoport D i h 4 _> nincs keresztező bordákkal.
Néhány tulajdonságai parciális rendezés tekintetében a planaritásának Hasse-diagram (azaz lehetősége rajzolni keresztezése nélkül élek):
- Ha a parciális rendezést egy rács. akkor lehet levonni keresztezése nélkül, ha, és csak akkor, ha a méret a sorrendben legalább két [3] [4].
- Ha részleges érdekében legalább egy minimális vagy maximális egy elem, lehetőség van a lineáris idő, hogy ellenőrizze, hogy nincsenek kereszteződések rajz [5].
- Határozza meg, hogy a részleges bemutatása érdekében a sík Hasse diagram általában NP-teljes probléma [6].
- Ha meghatározott y -coordinates részleges érdekében elemek, a lineáris idő megtalálható annak Hasse diagramot megőrzése megadott koordináta, kivéve, ha a rajz van [7]. Különösen, ha egy adott sorrendben szinten lehet lineáris időben meghatározni, hogy Hasse-diagram nincs csomópontok, ahol a magasság minden csúcsa arányos a rangsorban.