Meghatározása Hasse-diagramok rács
Így, az összes pár azonosított inf és sup. Ennélfogva, nézett Hasse diagram - rács.
Ellenőrizni, hogy ez a moduláris rács, úgy vertex 2, 4 és 5:
Ez elosztó rács nem, mivel nem moduláris.
Rajzolj egy diagram a rács Hasse osztója 14. képez rács, ha ez a logikai algebra? Ha igen, hány elemében. Ez egy egyszerű univerzális algebra?
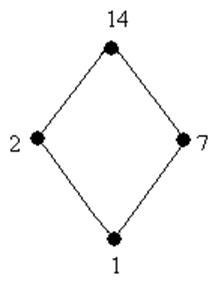
Határozza meg, hogy a rács alkotja a logikai algebra. A Boole-algebra teljesítéséhez szükség van a következő feltételeknek:
1) rácsos elosztó
1) rács elosztó, mivel nem tartalmaz semmilyen sublattice típusa:
Ennélfogva, a rács képez Boole algebra.
Készítünk egy kongruencia rács a következő elv:
Megjegyezzük, hogy ha, akkor az azonos osztályba kell birtokolnia és elemei 2 és 7, így kap.
Így a kongruencia rács a formája:
Ahhoz, hogy az egyetemes algebra ez egy egyszerű kongruencia rács tartalmaznia kell csak a szélső elemeket. Következésképpen az UA nem egyszerű.
Legyen N = á, * n - univerzális algebra természetes számok munkafolyamatban. Tekintsük az elemek 384 és 4374 E algebra és jelentésük A részalgebra által generált ez a két elem.
Majd a szám 60466176 tartozik ehhez részalgebra?
Mi számának növelését faktoring:
A táguló elem van jelen, kevesebb, mint azok, amelyek alkotnak részalgebra, és így nem tartozik hozzá, ezért a szám 60466176 nem yavlyatsya subalgebras elem B.
Tekintsük a csoport maradék Z231 additív csoportja Z az egész számok modulo száma 231.
Határozza meg a kongruencia rács a csoport.
Ez egyszerű?
-egész számok csoportját modulo 33
Kapjuk a következő rács:
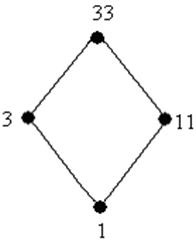
kongruencia rács (. lásd 2. feladat) az alábbi formában:
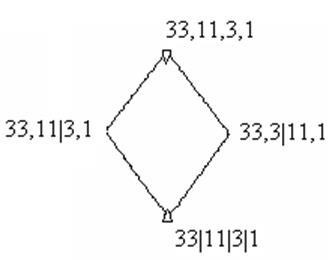
Mivel a kongruencia rács, továbbá a szélsőséges elemeket tartalmaz más, mint egy univerzális algebra nem egyszerű.
Univerzális algebra Z231 a korábbi probléma pryamorazlozhimoy?
Következésképpen ez az univerzális algebra közvetlenül felbontható.
hogy a legkülönbözőbb formákban következő sor: számok csoportját Zn univerzális algebra osztály?
Nem, ez nem felel meg az axióma kiegészítők termékcsoport a maradék osztályok.
Az Oktatási Minisztérium és a tudomány
Algebra Tanszék és matematikai logika