Értékelése megbízhatóság korrelációs együttható
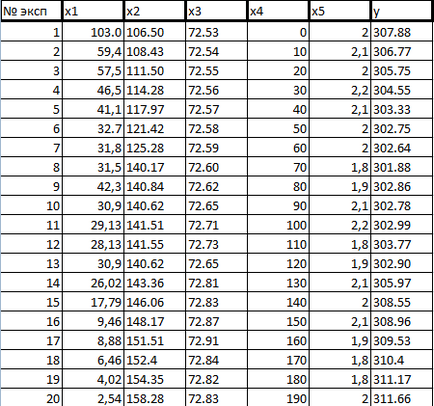
Érvényességének vizsgálata a korrelációs együttható
Lineáris korrelációs együttható, kiszámítani mintavétel egy véletlenszerű változó. A mintából nyert korrelációs együttható r egy becslés korrelyatsiir tényező a lakosság körében. A csökkenés a megfigyelések száma megbízhatóságát a korrelációs együttható esik. Értékelése jelentőséggel (szignifikancia) a lineáris korrelációs együttható összehasonlításán alapul a r értékeket annak átlagos négyzetes hiba:
,
Az jelentőségének értékelése során a korrelációs együttható általában úgy a következő helyzetet.
1. Ha a megfigyelések száma elég nagy (általában 30 év fölöttiek), és az értéke a korrelációs együttható kisebb, mint 0,9, a megoszlása a korrelációs együttható r tekinthető közelítőleg normális, az átlagos négyzetes hiba
,
Ha kellően nagy számú megfigyelés r meg kell haladnia az átlagos hiba nem kevesebb, mint három alkalommal. Ha ez az egyenlőtlenség nem teljesül, akkor a kapcsolat fennállása megjelölések között nem tekinthető bizonyítottnak.
Feltételezve, hogy egy bizonyos valószínűséggel meg tudjuk konstruálni konfidenciahatárokat r:
.
Például, egy valószínűsége 0,95, amelyre t = 1,96, konfidenciahatárt összeget
,
Amikor a valószínűsége 0,997, amelyre a megbízhatósági tényezője t = 3, az összeg konfidenciahatárok
Mivel az r értéke nem haladhatja meg az egyik, majd ha> 1, jeleznie kell, csak az alsó határ, azaz azt állítják, hogy az igazi r nem kevesebb, mint.
2. A minta kis mérete, eloszlása távoli r a normális, más módszereket használnak, hogy értékelje a jelentősége a korrelációs együttható. Egy kis megfigyelések száma (n<30), средняя ошибка линейного коэффициента корреляции находится по формуле:
,
és annak fontosságát, ellenőrizhető a Student-féle t-próba. Ebben a hipotézise korrelációs együttható nullával egyenlő, azaz nincsenek összefüggést y és x az általános populációban. Ez használ statisztika:
,
becsült értéke, amelyet összehasonlítva a táblázat Student eloszlás táblázatokat. Ha a nullhipotézis igaz, azaz r = 0, akkor az elosztó t - próba Student eloszlás engedelmeskedik CN-2 szabadsági fok és elfogadott szignifikancia szintjét (általában 0,05). Minden egyes esetben, a forgalmazás táblázat Student-féle t-teszt egy olyan táblázat (kritikus) értéket t. amely szerint megengedhető a null hipotézist, és azt összehasonlítjuk a tényleges (becsült) értékei t. . T ha analízis> .. ttabl a null hipotézist elvetjük, és jelentősnek lineáris együttható, és a kapcsolat x és y - elengedhetetlen. És fordítva.
3. Ha egy kis megfigyelések száma a mintában, és a magas korrelációs együttható (r eloszlása eltér a normál), hogy ellenőrizze azt a hipotézist, korreláció és megalkotásához használt megbízhatósági intervallum z-transzformációs Fischer.
Erre a számított érték
.
A eloszlása Z közel van a normális. A variáció által kifejezett z
.
Számításaink zkritery 1. példa, mivel ebben az esetben van egy kis megfigyelések száma, a legmagasabb korrelációs együttható.
.
Nem logaritmusok az értékeket, akkor speciális táblázatok Z-transzformáció (Efimova MR 402. o., RA Shmoilova str.446, Eliseeva II str.473). Azt látjuk, hogy a korrelációs együttható = 0.94 sootvetstvuetZ 1.74.
Az arány a Z az átlagos négyzetes hiba 3. Így feltételezhetjük, hogy létezik egy valódi kapcsolat a kibocsátás értéke és az energiafogyasztás a teljes lakosság a vállalkozások.
A számítás a korrelációs együtthatók termelt STATISTICA programban.
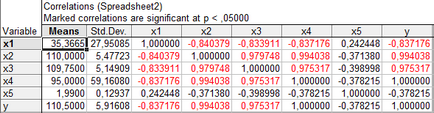
1. ábra - Korrelációs mátrix.
Az összefüggés határozza meg, hogy milyen mértékben a két változó értékét „arányos” egymással. Az arányosság azt jelenti lineáris kapcsolat. A korreláció magas, ha a gráf függőség „képviselhet” egy egyenes vonal (pozitív vagy negatív szögben). Tehát ez az egyszerű regressziós modell leírja a függőség egy változó az egyik tényező.
Megjegyzés: a fő jellemzői ennek a mutató.
Meg lehet venni a értékek -1 és +1. „+” Jel azt jelenti, hogy az összekötő vezeték (ha az érték egy változó növekszik, az értékek a többi változó is növeli), „-” azt jelenti, hogy a kapcsolat fordított.
Minél közelebb az arány 1, akkor a korrelációs együttható nagysága kisebb, mint 0,3 értékelik, mint egy gyenge láncszem, 0,31-0,5 - tisztességes, 0,51-0,7 - jelentős, 0,71-0,9 - szoros 0.91 vagy magasabb - nagyon közel van.
Ha minden változó növelése (csökkenése) azonos számú vagy azonos számú alkalommal, értéke a korrelációs együttható nem változik.
A korrelációs együttható - olyan mutató, amely értékeli a közelsége a lineáris összefüggés a jeleket.
Ha r = ± 1 jelentése lineáris összefüggés a funkcionális függőség. Ebben az esetben az összes megfigyelt értékek találhatók, egy közös vonalon. Úgy is nevezik, a regressziós egyenest. Ha R = 0 a lineáris korreláció nem elérhető. Ebben a csoportban az átlagos változó egybeesik a közös közeg, és a regressziós egyenes párhuzamos a koordináta tengelyekre.
Egyenlet r = 0 hiányát jelzi egy lineáris korreláció (korrelálatlan változók), de nem minden a összefüggés hiánya, továbbá, a statisztikai függőségek.
Ennek alapján a korrelációs együttható, nem tudjuk strogodokazat ok-okozati összefüggés a változók között, de mozheteopredelit hamis összefüggések t. E. korreláció, amely obuslovlenyvliyaniyami „egyéb” marad ki a látómezőt változók.
A fő probléma, hogy ál összefüggés az, hogy nem tudjuk,
aki az f # 1104; hordozót. Azonban, ha tudjuk, hogy hol kell keresni, akkor
használhatja a parciális korrelációk ellenőrzésére (részlegesen nem tartalmaz # 1104; csak olvasható) hatása határozza meg, # 1104; nnyh változók.
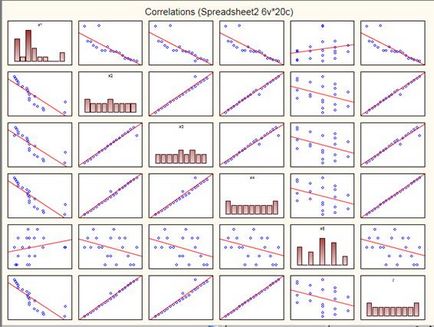
2. ábra - A scatterplots.