Előadás a témában geometria 2
1

2 szeterometria TÉMA: 2.3 Tetrahedron. RÉSZ tetraéder. AK VSUES tanár Boyko Vera Ivanovna

3. szakterület: „banki”, „Room Service” „Szolgáltatás hazai és kommunális szolgáltatások”, „Commodity és vizsgálata a minőségi fogyasztási cikk”

4. Követelmények a tudás, készségek és képességek 3. A tanulmány az előadások a hallgató tudni kell: * A koncepció a rendszeres poliéderek. * Meghatározása tetraéder és a képe. * Elemei a tetraéder. * Hogyan építsünk egy része a tetraéder. A tanulmány az előadás, a tanulók legyenek képesek: ábrázolása tetraéder. A probléma megoldása érdekében az épület egy tetraéder szakaszok.

6 poliéder felületet, amely sokszögek meghatározó geometriai test lesz az úgynevezett poliéder. Sok polyhedra nem találták az emberek, mint a természetben.

7 A tetraéder - felületet, amely négy háromszög Meghatározás
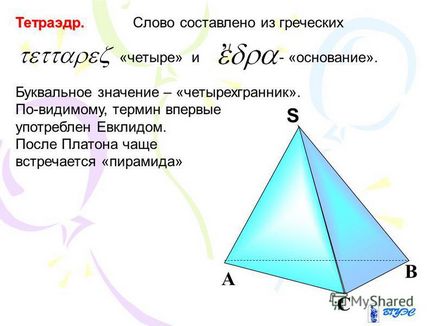
8 Tetrahedron. Tetraéder. Szó tagjai a görög „négy”, és - „az alap.” A szó jelentése - „tetraéder”. Úgy tűnik, a kifejezés először használt Euclid. Miután Platón több közös „piramis”, / C A B SS
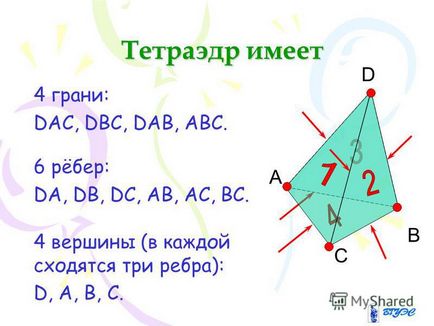
9 tetraéder négy arca: DAC, DBC, DAB, ABC. 6 bordák: DA, DB, DC, AB, AC, BC. 4 csúcs (minden három élek konvergálnak): D, A, B, C D A B C
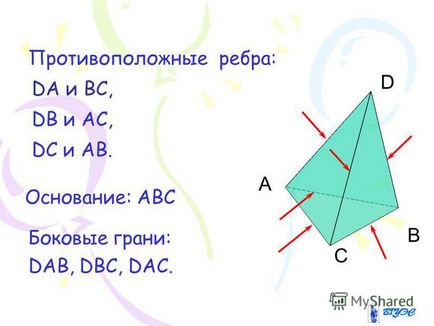
Szemközti szélei 10: A B C D DA és BC, DB és az AC, DC és az AB. Base: ABC oldalfalakon: DAV, DVS, DAS.

11 fényképek Tetrahedron A 0 B 0 C 0 D 0 - tetszőleges tetraéder, A, B, C és D - a párhuzamos nyúlványok csúcsa a képsík (π). A szegmensek AB, BC, CA, AD, BD, CD az oldalai és átlók az ABCD négyszög. Ábra által alkotott ezeket a szegmenseket (vagy bármilyen más alakú, mint ez) egy illusztráció a tetraéder A 0 B 0 C 0 D 0.
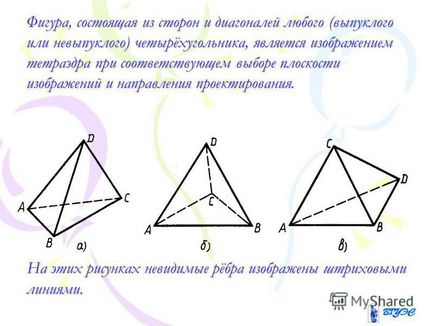
12. ábra, amely az oldalán és átlók bármely (nem domború vagy konvex) a négyszög egy képet megfelelő választás a tetraéder képsík és az irányt a vetítés. Ezeken a rajzokon a láthatatlan élek látható szaggatott vonalak.
13 A B C D M N M és N pontok - közepe élek AB és AC ABCD tetraédert. Bizonyítsuk be, hogy a vonal MN párhuzamos sík a VSD.
14. Mi a poligonok kaphat szakaszban. A tetraéder négy arcok keresztmetszetű lehet: háromszögek négyszögek
15 A B D C N M K magyarázni, hogyan kell építeni egy tetraéder DABC metszősík ponton áthaladó M, N, K megkeresése szekcionált kerülete, ha M, N, K - közép borda és minden éle a tetraéder egyenlő egy.
16 A B D C N M K magyarázni, hogyan kell építeni egy tetraéder DABC metszősík ponton áthaladó M, N, K megkeresése szekcionált kerülete, ha M, N, K - közép borda és minden éle a tetraéder egyenlő egy.
17 A B D C N M K magyarázni, hogyan kell építeni egy tetraéder DABC metszősík ponton áthaladó M, N, K megkeresése szekcionált kerülete, ha M, N, K - közép borda és minden éle a tetraéder egyenlő egy. E
18 A B D C NM K magyarázni, hogyan kell építeni egy tetraéder DABC metszősík ponton áthaladó M, N, K E MN AC
19 Tetrahedron Construct Tetrahedron metszeti síkban ponton áthaladó M párhuzamos (FAA). A B C D M K P
20 Construct tetraéder metszősík ponton áthaladó T, P, D B C D D X R T M
21 Egy közepes-bordák AB és BC tetraéder SAVS tartott síkjával párhuzamosan a szélén a SB. Bizonyítsuk be, hogy ez a sík metszi a határán SAV és az SVS párhuzamos vonalak. C S A V E K MN adják: SAVS tetraéderek, MA = CF BN = NC,
22 Döntetlen DABC tetraéder éleit és a DB, DC, BC és jelölje rendre rámutat M, N és C Construct metszéspontja a vonal KN és ABD síkban. A B C D K N M M 1
23 1. feladatban élek AB, BD és a CD ABCD tetraéder megjelölt pontokat M, N és P Construct tetraéder MNP síkban.
24 döntés. Készítünk egy első egyenes, amelyen MNP metszi a sík arcok ABC. A lényeg az M a közös pont ezeket a gépeket. A konstrukció egy általánosabb pont NP továbbra szegmensek BC és azok kereszteződés egy ponton E, amely a második közös pont és MNP ABC síkok.
25 1. opció 1 Építés Probléma metszéspontja a vonal AB MNK síkon. A B D K N M
26 1. opció 1 Építés Hibás válasz metszéspontja a vonal AB MNK síkon. B N A D K M X
27 1. lehetőség 2. feladat Construct Tetrahedron metszősík ponton áthaladó A, B és C; A Je MND. A B D K N M C
28 1. lehetőség 2. feladat Construct válasz Tetrahedron metszősík ponton áthaladó A, B és C; A Je MND. A B D K N M C
29 2. lehetőség Task 1 Construct választ metszéspontja a vonal AB MDK síkban. A B D K N M X
Kiviteli alak: 30 2 Target 2 Construct Tetrahedron metszősík ponton áthaladó A, B és C; A Je NDK. A B D K N M C
Opció 2 31 2 Beépített Hibás válasz Tetrahedron metszősík ponton áthaladó A, B és C; A Je NDK. A B D K N M C
32
33 * tetraéder jellegű Egyes gyümölcsök, közülük négy pedig egyrészt vannak elrendezve tetraéder csúcsai közel a jobb oldalon. Ez a kialakítás annak a ténynek köszönhető, hogy a központok négy azonos golyókat, hogy összeértek, találhatók a csúcsai egy szabályos tetraéder. Ezért gyümölcs Hasonló alkotnak egy léggömb hasonló helyzeti viszony. Például, így lehet helyezni dió
34
Tetrahedron 35 formák egy merev, statikailag határozott design. Tetrahedron készült rudak, gyakran használják az alapja a térbeli tartószerkezet ível épületek, padlók, gerendák, rácsos hidak, és így tovább. D. A rudakat csak tesztelt hosszirányú terheléseknek. Egy téglalap alakú tetraéder alkalmazott optika. Ha a felületek, amelyek derékszögben, hogy fedezze a fényvisszaverő szerkezet vagy a teljes tetraéder olyan anyagból készül, erős fénytörés, hogy a hatást a teljes belső visszaverődés, a fény irányul egy arc szemközti felső derékszögű, tükröződni fog ugyanabba az irányba, ahonnan származik . Ez a tulajdonság létrehozásához használt sarok-cube reflektorok, katafotov.ugolkovyh otrazhateleykatafotov
36 tetraéderek mikrokozmosz víz, jég, H2O molekula metán CH4 molekula ammónia NH3 Diamond C - tetraéder egy él egyenlő 2,5220 Angström fluorit CaF2, tetraéder éle, mint 3, 8626 angström szfalerit, ZnS, tetraéder egy él egyenlő 3823 angström komplex ionok [ BF4] -, [ZnCl4] 2-, [Hg (CN) 4] 2-, [Zn (NH 3) 4] 2+.
37 teszt - Mi a poliéder, a felület? - Határozza meg a fő elemei a tetraéder. - Hány arca van, élek és csúcsok egy tetraéder? - Hogy poligonok kaphat egy részén tetraéder? - Hogyan építsünk egy szakasza tetraéder? - Ahol az élet találkozik egy tetraéder?