Tulajdonságai és alkalmazásai a kettős integrál
Funkciója két változó: \ (f \ left (\ right) \) \ (f \ left (\ right) \) \ (g \ left (\ right) \)
Független változók: \ (x \) \ (y \) \ (u \) \ (v \)
Kis lépésekben: \ (\ Delta \) \ (\ Delta \)
Régió integráció: \ (r \), \ (S \)
Tényleges számok: \ (a \), \ (b \), \ (c \), \ (d \), \ (\ alpha \), \ (\ beta \)
Polárkoordináták: \ (r \), \ (\ theta \)
Terület nagysága: \ (A \)
Terület: \ (S \)
test térfogata: \ (V \)
Súly lemezek: \ (m \)
Plate Sűrűség: \ (\ rho \ left (\ right) \)
Az első pillanatokban: \ (\) \ (\)
tehetetlenségi nyomatéka: \ (\) \ (\) \ (\)
A töltés lemez: \ (Q \)
Töltéssűrűségének: \ (\ sigma \ left (\ right) \)
A koordináták a tömegközépponti: \ (\ bar x \), \ (\ bar y \)
Az átlagos értéke a függvény: \ (\ mu \)
A kettős integrál függvény \ (f \ bal (\ right) \) a négyszögletes régió \ (\ left [\ right] \ alkalommal \ left [\ right] \) úgy definiáljuk, mint a határérték az integrál összeg (Riemann összeg):
\ (\ Megkövetelése \ nagy \ iint \ limits_ \ right] \ times \ left [\ right]> \ normalsize \ right) dA> = \ lim \ határok _ \, \ Delta \ 0 \\ \ text \, \ Delta \ 0 >> \ sum \ limits_ ^ m ^ n,> \ right) \ Delta \ Delta >>, \)
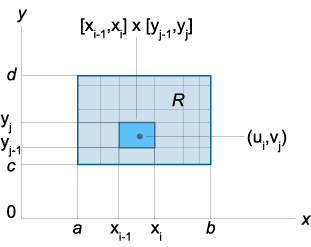
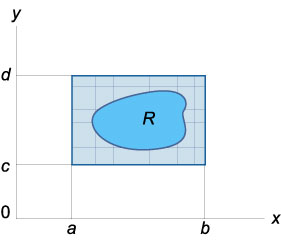
A kettős integrál függvény \ (f \ bal (\ right) \) egy tetszőleges területen \ (r \) határozzuk meg, mint a \ (\ nagy \ iint \ limits_R \ normalsize \ right) dA> = \ nagy \ iint \ limits_ \ right] \ times \ left [\ right]> \ normalsize \ right) dA>, \)
ahol téglalap \ (\ left [\ right] \ alkalommal \ left [\ right] \) régiót tartalmaz \ (r \), a függvény \ (g \ bal (\ right) = f \ bal (\ right) \), ha \ (f \ bal (\ right) \) van \ (r \), és \ (g \ bal (\ right) = 0 \) másképp.
A kettős integrál összege funkciók az összege integrálok ezeket a funkciókat:
\ (\ Large \ iint \ limits_R \ normalsize \ jobb) + g \ bal (\ right)> \ right] dA> = \ nagy \ iint \ limits_R \ normalsize \ right) dA> + \ nagy \ iint \ limits_R \ normalsize \ right) dA> \)
A kettős integrál különbség funkció a különbség az integrálok ezeket a funkciókat:
\ (\ Large \ iint \ limits_R \ normalsize \ right) - g \ left (\ jobbra)> \ right] dA> = \ nagy \ iint \ limits_R \ normalsize \ right) dA> - \ nagy \ iint \ limits_R \ normalsize \ right) dA> \)
A konstans együttható vehető jeleként a kettős integrál:
\ (\ Large \ iint \ limits_R \ normalsize \ right) dA> = k \ nagy \ iint \ limits_R \ normalsize \ right) dA> \)
Ha \ (f \ bal (\ right) \ le g \ left (\ jobbra) \) a \ (r \), majd az egyenlőtlenséget
\ (\ Large \ iint \ limits_R \ normalsize \ right) dA> \ le \ nagy \ iint \ limits_R \ normalsize \ right) dA> \)
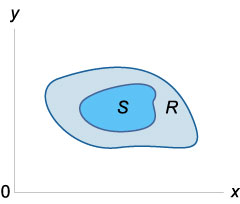
Ha \ (f \ bal (\ right) \ ge 0 \) a \ (r \) és \ (S \ részhalmaza R \), majd a
\ (\ Large \ iint \ limits_S \ normalsize \ right) dA> \ le \ nagy \ iint \ limits_R \ normalsize \ right) dA> \)
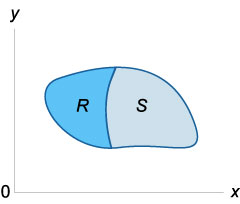
Ha \ (f \ bal (\ right) \ ge 0 \) a \ (r \), és a \ (r \) és \ (S \) - a nem-átfedő területet,
\ (\ Large \ iint \ limits_ \ normalsize \ right) dA> = \ nagy \ iint \ limits_R \ normalsize \ right) dA> + \ nagy \ iint \ limits_S \ normalsize \ right) dA> \)
Itt, \ (\) az Unió a domének az integráció \ (r \) és \ (S \).
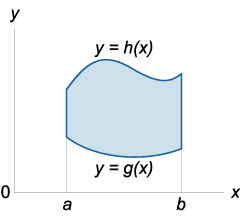
ahol az integráció régió \ (r \) úgy határozzuk meg, egyenlőtlenségek
\ (R = \ left \<\left( \right) \mid a \le x \le b,\;p \left( x \right) \le y \le q\left( x \right)\right\>\).
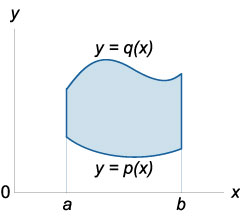
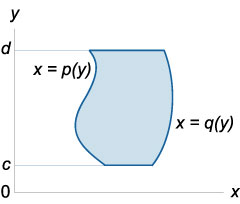
ahol az integráció régió \ (r \) úgy határozzuk meg, egyenlőtlenségek
\ (R = \ left \<\left( \right) \mid u\left( y \right) \le x \le v\left( y \right),\;c \le y \le d \right\>\).
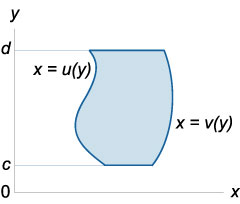
A kettős integrál téglalap alakú terület
Ha \ (r \) egy téglalap alakú terület \ (\ left [\ right] \ alkalommal \ left [\ right] \), majd a
\ (\ Large \ iint \ limits_R \ normalsize \ right) dA> = \ nagy \ int \ limits_a ^ b \ normalsize \ right) dy >> \ right) dx> = \ nagy \ int \ limits_c ^ d \ normalsize \ right ) dx >> \ right) dy> \)
\ (\ Large \ iint \ limits_R \ normalsize \ right) dxdy> = \ nagy \ iint \ limits_R \ normalsize = \ left (> \ right) \ left (> \ right) \)
polárkoordinátás
\ (X = r \ cos \ theta, y = r \ sin \ theta \)
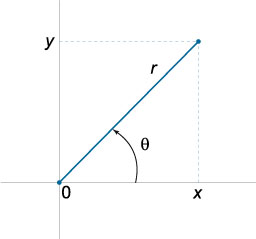
A kettős integrál polárkoordinátákban
Eltérés \ (dxdy \) polár koordinátákkal adják
\ (Dxdy = \ left | \ right) >> \ right) >> \ normalsize> \ right | drd \ theta = rdrd \ theta \)
\ (\ Large \ iint \ limits_R \ normalsize \ right) dxdy> = \ nagy \ int \ limits_ \ alpha ^ \ beta \ normalsize ^ \ normalsize \ right) rdrd \ theta >> \)
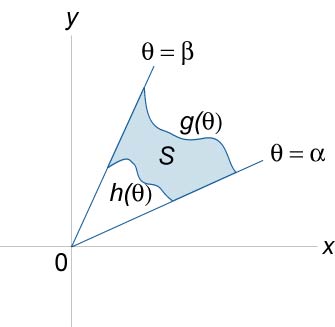
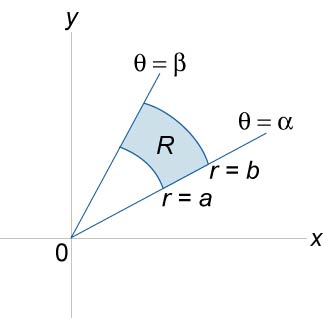
A kettős integrál poláris téglalap
Ha az integráció régió \ (R \) egy poláris téglalap. adott egyenlőtlenségek \ (0 \ le egy \ le r \ le b \), \ (\ alpha \ le \ theta \ le \ beta \), ahol a \ (\ beta - \ alpha \ le 2 \ pi \), majd a kettős integrál
\ (\ Large \ iint \ limits_R \ normalsize \ right) dxdy> = \ nagy \ int \ limits_ \ alpha ^ \ beta \ normalsize \ right) rdrd \ theta >> \)
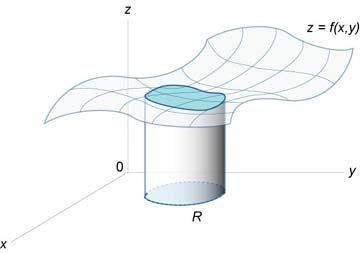
A kötet a test
\ (V = \ nagy \ iint \ limits_R \ normalsize \ right) dA> \)
\ (V = \ nagy \ iint \ limits_R \ normalsize \ right) dA> = \ nagy \ int \ limits_a ^ b \ normalsize ^ \ normalsize \ right) dydx >> \) Ha \ (r \) egy olyan terület típusú \ (II \) és vonallal körülhatárolt \ (y = c \), \ (y = d \), \ (x = q \ left (y \ right) \), \ ( X = p \ bal (y \ right) \), majd a
\ (V = \ nagy \ iint \ limits_R \ normalsize \ right) dA> = \ nagy \ int \ limits_c ^ d \ normalsize ^ \ normalsize \ right) dxdy >> \)
A kötet a test a két felület között
Ha \ (f \ bal (\ right) \ ge g \ left (\ jobbra) \) a \ (r \), akkor a test közötti térfogat felületek \ (\ left (\ jobbra) \) és \ (\ left ( \ right) \) e területen egyenlő
\ (V = \ nagy \ iint \ limits_R \ normalsize \ right) - g \ left (\ jobbra)> \ right] dA> \)
Tegyük fel, a tartomány \ (S \) meghatározott polár koordinátákkal a síkon \ (Oxy \) és vonallal körülhatárolt \ (\ theta = \ alpha \), \ (\ theta = \ beta \), \ (r = h \ bal (\ theta \ right) \), \ (r = g \ left (\ theta \ right) \). Tegyük fel továbbá, hogy a \ (S \) kap egy függvény \ (f \ left (\ right) \). Ezután a terület a mező \ (S \), és a térfogata a szilárd határolt felületi \ (f \ bal (\ right) \), által meghatározott képletek
\ (A = \ nagy \ iint \ limits_S \ normalsize = \ nagy \ int \ limits_ \ alpha ^ \ beta \ normalsize ^ \ normalsize>, \; \; V = \ nagy \ iint \ limits_S \ normalsize \ right) rdrd \ theta> \)

lemez Tömeg
\ (M = \ nagy \ iint \ limits_R \ normalsize \ right) dA> \)
A lemez helyezkedik el a \ (r \), és sűrűsége a ponton \ (\ right)> \) egyenlő a \ (\ right)> \).
A statikus pillanatok a lemez
Nyomaték lemez tengelye körül \ (Ox \) úgy határozzuk meg, a képlet
\ (= \ Large \ iint \ limits_R \ normalsize \ right) dA> \)
Hasonlóképpen, a pillanatban a tengelye a lemez \ (Oy \) van kifejezve
\ (= \ Large \ iint \ limits_R \ normalsize \ right) dA> \)
A tehetetlenségi nyomatéka a lemez
A tehetetlenségi nyomaték a lemez tengelyhez képest a \ (Ox \) kiszámítása a következő képlettel
\ (= \ Large \ iint \ limits_R \ normalsize \ rho \ left (\ right) dA> \)
A tehetetlenségi nyomaték a lemez tengelyhez képest a \ (Oy \) jelentése
\ (= \ Large \ iint \ limits_R \ normalsize \ rho \ left (\ right) dA> \)
Polar tehetetlenségi nyomaték adják
\ (= \ Large \ iint \ limits_R \ normalsize + \ right) \ rho \ left (\ right) dA> \)
A töltés lemez
\ (Q = \ nagy \ iint \ limits_R \ normalsize \ right) dA> \),
ahol az elektromos töltés van elosztva a tartomány \ (r \), és a sűrűség a ponton \ (\ right)> \) egyenlő a \ (\ right)> \).
A középérték függvény
\ (\ Mu = \ nagy \ frac \ iint \ limits_R \ normalsize \ right) dA>, \; \), ahol \ (S = \ nagy \ iint \ limits_R \ normalsize \).