A szekvenciát négyszögletes impulzusok - studopediya
Az első jel tekinthető szekvenciáját négyszögletes impulzusok időtartama amplitúdójú A. # 964; és ismétlési periódus T. A eredete alkalommal veszi közepén található az impulzus (ábra. 1.3).
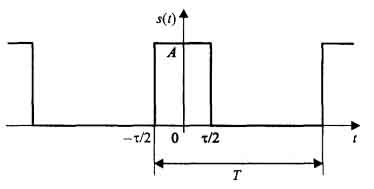
Ábra. 1.3. A periodikus szekvenciája négyszögletes impulzusok
Ez a jel egy még funkciót, így a képviseletére kényelmesebb szinusz-koszinusz formája a Fourier-sor - csak a koszinusz kifejezések ak lesznek jelen benne. egyenlő
Óvatosan vizsgálva a kapott általános képletű látható, hogy az impulzus időtartama és az időszak az ismétlés benne foglalt nem válik el egymástól, hanem kizárólag arányként. Ez a paraméter - az arány az időszak impulzushosszukat - úgynevezett munkaciklusa pulzus szekvencia, és betűvel jelöljük q. q = T / # 964;. Bemutatjuk ezt a paramétert Ebben a képletben az együtthatók a Fourier-sor, majd adja a képletet formájában sin (x) / x:
Néha porozitás helyett a visszatérési érték az úgynevezett kitöltési tényező (működési ciklus), és egyenlő az # 964; / T.
Most tudjuk írni és önálló képviseletét sorozata négyszög impulzus, mint a Fourier-sor:
Amplitúdóinak a harmonikus kifejezések a sorozat számától függ harmonikusok a törvény szerint sin (x) / x (ábra. 1.4).
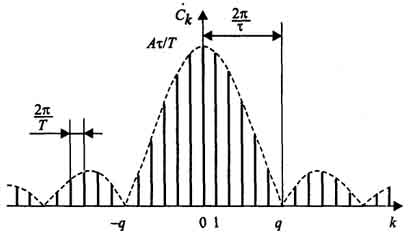
Ábra. 1.4. A Fourier-sor együtthatók négyszögletes impulzussorozat
Ütemezés funkció sin (x) / x még szirmú karaktert. Szólva a szélessége ezen lebeny, hangsúlyozni kell, hogy a két lehetséges vízszintes tengely kalibrációs spektrumok diszkrét periodikus jelek grafikonok - a harmonikus szám, és frekvenciákat. Ábra. 1.4 osztások tengely felel meg a számok a felharmonikusok, és a frekvenciaspektrumot paraméterek ábrázoljuk méretvonalak.
Így, a szélessége a lebeny mért száma harmonikusok egyenlő a munkaciklusát szekvencia (ha k = NQ van sin (πk / q) = 0, ha n ≠ 0). Ezért fontos jellemzője egy négyszögletes impulzussorozat - nem tartalmaz (nulla amplitúdójú) harmonikus szám, többszörösei a kitöltési tényezőt.
A távolság jelentése a szomszédos harmonikusok az impulzus ismétlési frekvenciája megegyezik - 2π / T. Spektrális szélessége szirmok, mértékegysége a frekvencia, egyenlő 2π / # 964;, hogy fordítottan arányos az impulzus időtartam. Ez, mint látni fogjuk, egy megnyilvánulása az általános szabályok - a rövidebb a jel, a szélesebb spektrumát.