A szavak a levelet a Poynting vektor egyetlen gördülő sorban a szögsebessége szögelfordulás
Poynting vektor,
Poynting vektor
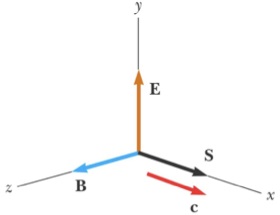
- vektor energia fluxus sűrűsége az elektromágneses mezőt. iránya a vektor egybeesik a terjedési irányát az elektromágneses hullám. Modul vektor átadott energia egységnyi idő keresztül egységnyi területen szokásos, hogy a terjedési irányát elektromágneses energia. Poynting vektor S vektor termék a villamos E és mágneses H mezők:
S = E × H.
Mért W / m ².
Poynting vektor áramlás egy zárt felület határoló egy töltött részecske rendszert, meghatározza az energia mennyisége elvesztette a rendszer által egységnyi idő miatt a sugárzás az elektromágneses hullámok.
♦ A Poynting vektort
♦ Vector Poynting
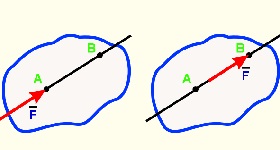
- vektor, amely ekvivalens egyenlő, hogy egy vektor, található egy egyenesen. Csúszó vektorok, például, az alkalmazott erők egy teljesen szilárd test. Két egyenlő és helyezkednek el ugyanabban a sorban erők ugyanazon a merev test mechanikai hatás.
♦ Vector gördülő
Egy sor vektor,
sorban mátrix
mátrix kisbetűs
- mátrixot, amelynek csak egy sor. A méret ilyen mátrix 1 × n.
♦ A sorvektor
♦ Matrix sor
♦ Matrix kisbetűs
- vektor irányított rögzített tengely mentén a forgás az irányba, ahonnan a forgatás a test látható előforduló óramutató járásával ellentétes irányba, és numerikusan megegyezik az idő származéka a forgásszög a test. Mértékegysége a szögsebesség S-1 vagy rad / s.
♦ A szögsebesség vektor

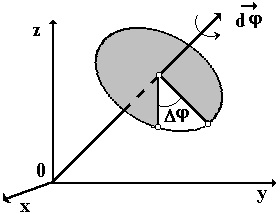
- vektor, amelynek nagysága egyenlő infinitezimális elfordulási szög, és az irányt jelzi az irányt a forgástengely úgy, hogy a forgás az óramutató járásával megegyező (iránya a vektor által meghatározott jobbkezes csavar szabály). Concept csak vektorok alkalmazhatók annak a végtelenül kicsi forgásszögek, önkényes forgatás szöge nem egy vektor.
♦ vektor szögelfordulási
- vektor megegyezik az idő-származékot a szögsebesség. Mértékegysége a szöggyorsulás vagy -2 rad / s².
♦ Vector szöggyorsulás

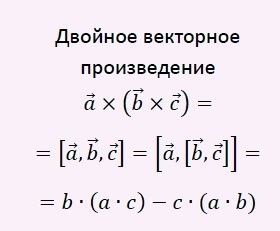
Vektor-skalár termék,
vegyes termék vektorok
- skaláris szorzata egy vektor egy vektor által a két termék más vektorok. Vektor-skalár eredmény (vegyes) terméket a három vektor skalár térfogatával egyenlő a paralelepipedon által alkotott ezek a vektorok, figyelembe a plusz jel a jobb oldali három vektorok és a mínusz jel a bal oldali három vektorok.
Vektor-skalár Properties (vegyes) termék:
- - vektor-skalár termék nulla, ha a coplanarity (koplanáris párhuzamosság) a három vektor;
- - kevert termék nem változik, ha felcserélni a jelei a vektor és skalár szorzás
egy ⋅ (B × c) = (a × b) ⋅ c - - vektor-skalár termék nem változik, amikor a permutáció a vektorok egy kör alakú módon
egy ⋅ (B × C) = b ⋅ (C × a) = C ⋅ (A × b) - - a csomópont bármely két vektor vektor-skalár termék előjelet
egy ⋅ (B × C) = - b ⋅ (A × c) - - egy Descartes-féle derékszögű koordináta-rendszer, amely egy vektor-skalár termék meghatározó sorok, amelynek elemei egyenlő a koordinátáit a vektorok megszorozva.
♦ vektor-skalár termék
♦ vegyes termék vektorok
- egy régióban a tér, vagy sík, amelyben minden pont kap egy vektorral mennyiséget. Vektor mezők területen erők, sebességek, mágneses indukció, és a t. D.
♦ A vektor mező

Vector termék,
termék külső
- működését a két a és b vektorok. az eredmény az, amely merőleges vektor C megszorozzák mindkét vektorral, a modul a termék a modulusok ezen vektorok által szinuszával a köztük lévő szög, és az irányt úgy, hogy a jobb oldali van kialakítva tripla vektorok egy. b. c:
| C | = | A |⋅| B |⋅sinφ
A leggyakrabban használt „vektor termék” és a „külső termék” nagyon ritkán.
Az elnevezés a vektor termék a vektorok a és b:
a × b vagy [AB]
- a × a = 0;
- a × b = - b × A;
- (k⋅a) × b = a × (k⋅b) = k⋅(A × b) (tekintettel a asszociatív tulajdonsága numerikus tényezővel);
- (A + b) × a = a × c + b × c (forgalmazó relatív mennyiségét vektorok tulajdonság).
- - egyenlőség nullára a vektor termék egy szükséges és elégséges feltétele a kollinearitást két vektor;
- - hossza (modul) A vektor termék számszerűen egyenlő a terület a paralelogramma épített szorzatát vektorok leadott egy közös eredetű;
♦ A vektor termék
♦ A külső termék
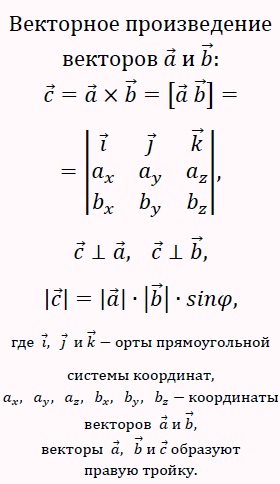
♦ A vektor potenciál

vektor potenciál
elektromágneses mező
- vektor funkció A (x, y, z, t), a forgórész (vortex), amely egyenlő a vektor a mágneses indukció B egy elektromágneses mező megfontolás alatt:
B = ∇ × A = rothadás A
♦ A vektor potenciál az elektromágneses mező

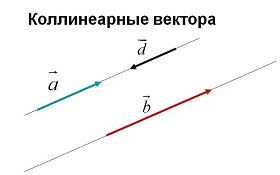
- vektorok feküdjön párhuzamos vonalak, vagy ugyanazon a vonalon. A szükséges és elégséges feltétele a kollinearitást két nem nulla vektorok arányos a koordináták (lineáris függés vektorok), vagy eltűnő a vektor termék. A skaláris szorzata kollineáris vektorok egyenlő a termék a hosszuk, hozott a plusz jel, ha a vektorok ugyanabba az irányba, és a mínusz jel ellenkező irányban e vektorok. A nulla vektor kollineáris minden vektor. Elfogadható, de nem ajánlott, kollineáris vektor nevezzük párhuzamos.
♦ kollineáris vektorok