Class 10, az anyagot a leckét, négyszögletes parallelepipedon, előadás tartalom platform
Ez az úgynevezett téglatest prizma, amelynek alapja egy paralelogramma.
Paralelogramma, amely alkotja a doboz, az úgynevezett lapján. saját oldalán - bordák. és a csúcsokat paralelogramma - top box. Minden részletét a doboz - paralelogramma.
Parallelepipedonok lehet közvetlen és ferde.
Általában különbséget bármely két szemközti oldalon, és felhívta a bázisok. és a másik oldalon - az oldalsó felületek a doboz. Élek a téglatest, nem tartoznak az alapon, a továbbiakban oldalsó széleit.
Két arc a dobozt, amelynek a közös él, azt mondta, hogy a szomszédos. és nincs közös élek - szemben.
Összekötő szakasz két csúcsot nem tartozó egyik oldalán, az úgynevezett átlós a doboz.
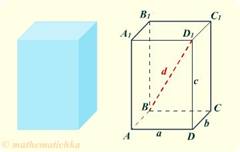
Közvetlen téglatest, amelynek alapja a téglalap hívják hasáb alakú. Minden részletét egy téglatest - téglalapok.
Hosszúságú párhuzamos szélei egy derékszögű paralelepipedon nevezzük annak lineáris méretei (méretek). A téglatest három lineáris méretét.
· A szemben lévő oldala a doboz egyenlő és párhuzamos.
· Mind a négy átlós téglalap metszi egy ponton, és ossza ezt a pontot a felét.
· Az oldalsó széle a doboz közvetlenül - téglalapok.
· Átlós négyzet téglatest egyenlő a négyzetének összege a három dimenzióban. D2 = a 2 + b 2 + c 2.
Nézzük a rövidség kedvéért nevezzük ezt a képletet „háromdimenziós Pitagorasz-tétel”.
A terület egy téglatest
Formula felülete téglatest
ahol S - területe egy derékszögű paralelepipedon,
Formula téglatest térfogata V = a • b · h
Kuba területén
A felülete kocka
Formula kocka területen S = a2 6
ahol S - területe a kocka,
Egy - a hossza az arc a kocka.
térfogatú kocka V = a3
Algoritmus a problémák megoldására:
1. Felhívjuk a téglatest. Nem feltétlenül a skála, akkor kézzel.
2. Bejelentkezés a csúcson. Megjegyezzük, az ábrán említett feltétellel pontot. Elhelyezés a vonalakon, ahol szükséges.
3. Tegyen egy ismert (előre meghatározott) értéket közvetlenül a rajzban.
4. Ha egy háromszög a testben, akkor azt találjuk, hogy van-e megfelelő szögben benne, és mi volt az. Ehhez használjuk a tételek a síkjára merőleges vagy három merőlegesek.
5. Felhívjuk a háromszög a gépen. Azt is felismerik a meghatározott és a kívánt értéket, ha szükséges, hordozó számos párhuzamos bordák.
6. elvégzi a szükséges számításokat az ismert képletek. Jellemzően ez lesz a Pitagorasz-tétel és a meghatározása a szinusz és koszinusz az akut szögek a derékszögű háromszög.
A kulcsfontosságú.
B9 № 245359. megtalálni a távolság négyzetével közötti csúcsok C és A 1 egy derékszögű paralelepipedon, amelyre AB = 5, AD = 4, az AA 1 = 3.
Határozat.
Vegyünk egy derékszögű háromszög, amelyben a átfogója. A tétel Pitagorasz
A dobozban - átlós, =. ennélfogva
B9 № 245361. Keresse szög a hasáb alakú, amelynek ,. Adja meg a választ fokban.
A hossza egy téglalap átlója, Pitagorasz-
Egyenlő szárú derékszögű háromszög: így annak éles szögek egyenlőek
B9 № 245363. Ide szöge derékszögű paralelepipedon, amelynek = 4 = 3 = 5. Adja meg a választ fokban.
Vegyünk egy derékszögű háromszög pitagoreusi
Tekintsünk egy derékszögű háromszög Mivel = =, akkor a háromszög egyenlő szárú, akkor a bázis szögek egyenlőek.
9 № 271071. Keresse meg a távolság négyzetével csúcsai között, és a téglatest, hogy.
Határozat.
Vegyünk egy derékszögű háromszög, amelyben az átfogója, és határozza meg a tér hossza Pitagorasz-tétel
A négyzetes - átlós. ennélfogva
B9 № 271571. Keresse meg a távolságot a csúcsok és a téglatest, hogy.
Határozat.
Vegyünk például egy háromszög, amelyben a átfogója és megtalálni annak hossza a Pitagorasz-tétel:
B9 № 272551. Keresse szög a hasáb alakú, amelynek ,. Válasz adni fok.
Határozat.
Vegyünk egy derékszögű háromszög, van Pitagorasz-
Vegyünk egy derékszögű háromszög Mivel a háromszög egyenlő szárú, akkor a bázis szögek egyenlők.
Ezt a leckét - Workshop
B9 № 245360. Find a távolság a csúcsok az A és D a négyszögletes parallelepipedon hogy AB = 5, AD = 4, AA = 3.
B9 № 245362. Ide szöge derékszögű paralelepipedon, amelynek = 5 = 4 = 4. Adja meg a választ fokban.
27055. A terület felszíne kocka egyenlő 18. Keresse átlója.
Képzési anyagok a leckét
270527. Keresse meg a távolság négyzetével csúcsai között, és a téglatest, amelynek ,,.
271075. Keresse meg a távolságot a csúcsok és a téglatest, amelynek ,,.
285399.V derékszögű paralelepipedon ismert, hogy ,. Keresse meg a hossza a borda.
271579. Keresse meg a szög a téglatest, amelynek ,,. Válasz adni fok.
271827. Keresse meg a szög a téglatest, amelynek ,,. Válasz adni fok.
272321. Keresse meg a szög a téglatest, amelynek ,,. Válasz adni fok.
245.359 Vizsgált tér közötti távolság a csúcsok és a téglatest, amelyre ,,.
245360. Keresse meg a távolságot a csúcsok és a téglatest, amelynek ,,.
245361. Keresse meg a szög a téglatest, amelynek ,,. A válasz hagyja a gradusah.2
245362. Keresse meg a szög a téglatest, amelynek ,,. Válasz adni fok.
245363. Keresse meg a szög a téglatest, amelynek ,,. Válasz adni fok.
27060. két szélét egy derékszögű paralelepipedon kinyúló egy csúcsot, értéke 1, és 2. A felülete a paralelepipedon egyenlő 16. megtalálja a diagonális.
27077. A kötet, amely derékszögű paralelepipedon egyenlő 24. Egy, az éle van 3. Keresse a terület az arc egy paralelepipedon merőleges ezen a szélen.
27079. két szélét egy derékszögű paralelepipedon kinyúló egy csúcsot, egyenlő a 2. és 6. A kötet a paralelepipedon egyenlő a harmadik borda 48. megkeresése paralelepipedon kilépő ugyanazon a csomóponton.
27080. Három szélei egy derékszögű paralelepipedon kinyúló egy csúcsot, egyenlő 4, 6, 9. Find szélén egyenértékű kocka vele.
27081. Hányszor térfogata nagyobb lesz a kocka, ha élek háromszorosára nő?
27082.Diagonal kocka. Megtalálja a hangerőt.