Tudd Intuíció, egy előadás, lineáris összefüggés a vektorok
Definíció 7. Ha (8.1) akkor kivitelezhető, ha az összes vektor a1. a2. aknazyvayutsyalineyno független.
Definíció 8. Ha az egyenlőség teljesül, akkor azt mondjuk, hogy a b vektor yavlyaetsyalineynoy kombinációja vektorok a1. a2. ak. ililineynovyrazhaetsya át ezeket a vektorokat.
Megjegyezzük, hogy ha a vektorok a1. a2. ak lineárisan függ, akkor legalább az egyik vektorok lineárisan kifejezve a másik. Ez következik a meghatározás 6, mintha legalább az egyik, akkor lehetőség van arra, hogy végezze el a többi osztály, és akkor mi lesz, ha. Ennek a fordítottja is igaz, hogy ha az egyik vektorok lineárisan kifejezésre a többi, ezek a vektorok együtt lineárisan függ.
Megjegyezzük, hogy ha az a és b vektorok nincs egy egyenesen vagy. b és c nem egy síkban vannak. akkor ezek a vektorok lineárisan függetlenek, illetve a síkban vagy térben.
Megmutatjuk ebben a példában három nem egy síkba eső vektorok a. b és c. Indirekt bizonyítás, feltételezve, hogy ezek a vektorok, de nem egy síkban vannak. de lineárisan függ. Ezután meg kell felelnie a feltétele lineáris függését vektorok, azaz és lehet egyidejűleg. Aztán, meg lehet osztani a bal és a jobb oldalon az egyenlet, és az eredmény egy kifejezés, amely ellentmond a meghatározása 10 ( „”), azaz Bár a vektorok a. b és c nem egy síkban vannak. de a vektor egy lineáris kombinációja a másik két B és C. amely azt mondja (meghatározott 8) azok lineáris kapcsolat. Ebből az következik, hogy egy vektort kell lennie lineárisan független vektor a b és c. Érdekes, hogy a háromdimenziós térben, bármely négydimenziós vektorok lineárisan függ.
Két nulla a és b vektorok merőleges. ha azok merőleges (a nyúlvány egy b vektor, és a nyúlvány a b vektor nulla). Akkor írj. Ilyen vektorok mindig lineárisan függetlenek.
Ha nem nulla vektort a. b és c értéke páronként merőleges, akkor alkotnak három lineárisan független vektor.
Definíció 9. Rangomsistemy vektorok a maximális számát a lineárisan független vektor.
Definíció 10. A lineáris tér nevezzük egy n-dimenziós. Ha talál n lineárisan független vektor, és bármely rendszer, amely egy nagyobb számú vektorok lineárisan függ ezt a helyet.
Például azok a vektorok, amelyek fekszenek egy egyenes vonal. alkotnak egy-dimenziós térben. amelyben csak az egyik független vektor. és az összes többit ki lehet fejezni lineáris egyenletek rajta. A gépen több vektort képez egy kétdimenziós térben. azaz Ebben a térben vannak meghatározva csak két független vektor.
Definíció 11. Ha a tér egy véges halmaza lineárisan független vektorok, akkor nazyvayutkonechnomernym. és ha talál, bármennyi lineárisan független vektorok - végtelen.
Definíció 12. Az n lineárisan független egység vektorok n-dimenziós térben nazyvayutbazisom n-dimenziós térben.
Megjegyezzük, hogy az alapja vektorok bármilyen más vektorok meghatározott ennek alapján ki lehet fejezni.
Tétel. Minden vektor X lineáris n-dimenziós térben ábrázolható egyedileg formájában egy lineáris kombinációja alapján vektorok.
Proof két részből áll. Kezdjük a lehetőséget, hogy kifejezze tetszőleges vektor alapján lineáris tér. majd, hogy a bomlás tetszőleges vektor alapján csak.
Tegyük fel, hogy egy önkényes alapot nR dimenziós tér, és egy tetszőleges vektor. Mivel minden n + 1 vektorok lineárisan független n R dimenziós tér (Definition 6), a rendszer képező vektorokat l1. l2. ln és X-nek kell lineárisan függ. Ez azt jelenti, hogy az egyenlőség
ahol - az egyidejűleg számos nem nulla. Egyértelmű, hogy, mivel egyébként legalább az egyik a számok nem lehet nulla, és így egyenletet (8.2) lenne formájában
, ami viszont. Úgy mutat lineáris függését alapján vektorok. Mi express x az egyenletben (8,2), elosztjuk a együtthatói li és mozgó őket a jobb oldalon. Elvégzése után az átalakítás van
Most bebizonyítjuk, hogy a tágulási (8.4) az x vektor alapján l1. l2. ln csak. Tegyük fel, hogy a vektor x a térben R két különböző bővítések
Majd vonjuk egymástól az egyenlőség, és mivel a bal oldali ugyanaz a vektor. megkapjuk az
Ezért van egy olyan rendszer
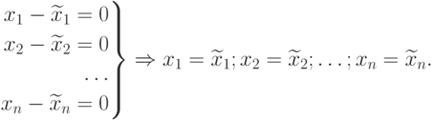
Az utolsó kifejezés teljesen bizonyítja a tétel.