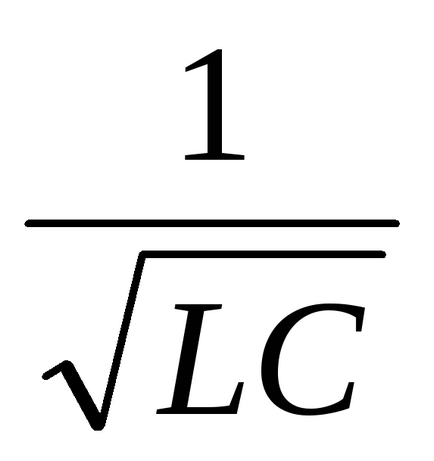Work № 4
A cél a munka -, hogy tanulmányozza a funkciók a tranziens folyamatok áramkörökben tartalmazó energiát tárolja, fogadó képviseletet létfeltételek steady-state mód a láncban, és kapcsolata az erőltetett módban.
1. A főbb rendelkezések az elmélet
Láncok, amelyek csak rezisztív elemek nem halmozódnak villamos energiát felhasználó közötti kommunikációt a reakció és hatását ismerteti állandó tényező, amely független a korábbi állapotát az áramkör és határozza meg a kapcsolat diagram és a paramétereket a rezisztív elemek.
Egy másik viselkednek villamosan láncokat tartalmazó meddő energia akkumulátorokhoz (induktivitás, kapacitás). Ebben az esetben az energiát, amelyet a források, vagy visszafordíthatatlanul átalakul egy másik fajta energiát fogyasztott, vagy ha munkát, vagy halmozódik fel a láncot a jet meghajtók. Ebben a láncreakció külső hatás nem csak attól függ, hogy milyen jellegű a hatása, hanem az energia tartalékok a jet meghajtók.
A kapcsolódó folyamatok változása az energiatárolás, az úgynevezett tranziens.
Gyakorlatilag az összes láncokat tartalmazó reaktív elemek, mindig a tranziens üzemmódban. Vannak azonban olyan rezsimek áramkörök, amelyek gyakorlatilag nem változik az energia tartalékok a reaktív elemek, vagy változtatni a periodikus törvény (ebben az esetben nem változik az átlagos energia érték az időszak alatt a reaktív elemek). Ezek a módok nevezzük kvázi állandósult vagy állandósult előforduló láncú források állandó vagy időszakos időben paramétereket.
Tranziensek lineáris elektromos áramkör által leírt lineáris differenciálegyenletek. A teljes megoldás ezen egyenletek szokták tekinteni az összeg a teljes és saját döntéseket. Egy különösen megoldás nem függ az energia tartalékok a jet elemek és határozza meg a külső forrásokból, valamint a konfigurációs paraméterek és áramköri elemeket. Ez az úgynevezett szűkített komponenst. A teljes megoldás döntően az állam jet hajt az energia tartalékok, alakja nem függ külső forrásokból, ez az úgynevezett szabad komponens.
Form megoldások szabad komponens függ a gyökerek a karakterisztikus egyenlet, és leírhatók, mint
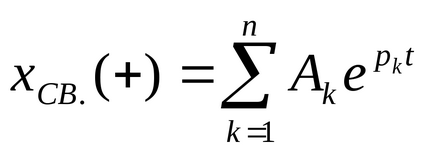
A létezése lineáris áramkörök gyökerek nulla valós része csak lehetséges áramkörök veszteség nélkül, amely csak reaktív elemek. Ebben az esetben a csillapítatlan rezgések keletkeznek az áramkörben. Mivel a gyakorlatban az ilyen hálózatok nem létezik, a tanulmány tisztán elméleti.
Különösen érdekesek azok a visszafordíthatatlan áramköri aktív elemekkel (opamp et al.), Amely abból a szempontból, a lánc lehet tekinteni, mint elemeket tartalmazó negatív paraméterekkel. Ebben az esetben a karakterisztikus egyenletnek gyökerek pozitív valós része, az ingyenes komponens növelheti a végtelenségig.
A tényleges áramkörök, ez a mód nem lehetséges, mert egy bizonyos ponton a lánc mozog nemlineáris üzemmódban, amely leállítja a további növekedés a szabad komponens.
Ebben a laborban, ilyen rendszerek nem veszik figyelembe. Mivel a passzív áramkörök veszteség mentes összetevő mindig csillapítani annak csillapítása becsült időtartama az átalakulási folyamat, amely bevezeti a folyamatos τ bomlás. τ - az időintervallumot, amelyben a szabad komponens után szeres faktorral csökken e (e = 2,71828 ...).
Az időtartam a tranziens általában egyenértékűnek tekintjük (3 ÷ 4) τ. Végén ebben az időben, a maradék értéke egyenlő a szabad komponenst századmásodpercekben a kezdeti érték.
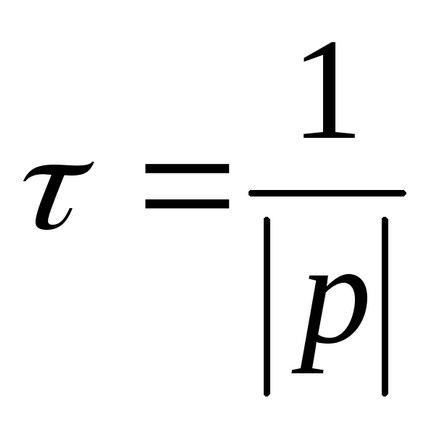
P1,2 = - δ ± јω. az idő által meghatározott állandó képlet
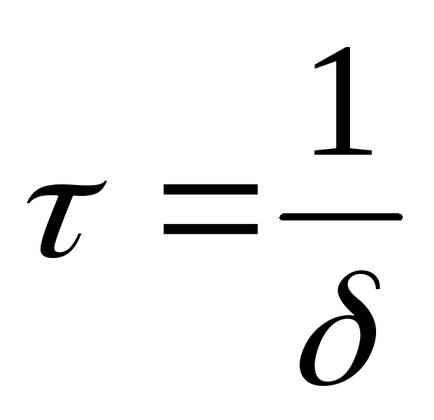
Tekintsük az adott tranziens áramkörök az első és másodrendű. Legvilágosabban tranziensek lehet tanulmányozni a lánc csatlakozik egy egyenáramú forrás. Mivel ebben az esetben, szükséges eleme van egy állandó értéket, a szabad komponenst tiszta formában izoláljuk, és megfigyelhető egy oszcilloszkópon képernyőn.
A laboratóriumi beállítási tanulmányozására tranziensek általánosan használt generátor négyszög impulzusokkal, ahol az impulzus időtartam (szünet) úgy választjuk meg, hogy hasonló volt az állandó tranziens időt.
Az impulzus ismétlési periódus T = 1 / f. ahol F - a mester oszcillátor frekvenciáját. Mivel impulsovti időtartama egyenlő a időtartamát a szünetek közöttük, TU = 1 / 2f.
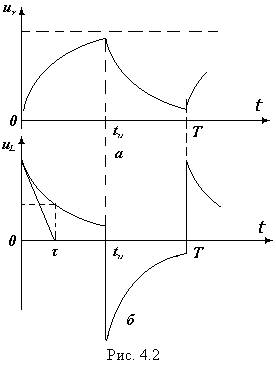
A számított egyenértékű áramkört, például áramköri R-L, a tartományban a ábrán látható impulzus 4.1, és megfelel a befogadás tsepir forrás Lc-EMF-állandója, és a szünet intervallum - a ris.4.1.b (rövidzár tsepir-L). Tipikus hullámformák A kísérlet ábrán mutatjuk be a 4.2.
Mivel az ellenállás, és a jelenlegi rnapryazhenie része csatlakozik egyenesen arányos zavisimostyuur = i · r. napryazheniyaur görbe (t) a megfelelő mértékű, és a jelenlegi görbe tsepii (t).
A hullámforma könnyen meghatározzuk az állandó τ idő alatt. Ez megegyezik a szegmens subtangent szerint felépített 4.2 ábra. (B). R-lánc Lpostoyannaya ravnaL / r időt. A tsepir S - velichinerC. Pontosabban a hullámforma, hogy meghatározza az időállandó alapján ezt. mint azt már korábban említettük. ideje alatt a τ szabad komponens csökken ve = 2,72 és körülbelül 0,37 a maximális érték (ris.4.2.b). Mindenesetre, először meg kell meghatározni a időskálán erre hullámforma (velichinaT = 1 / f ismert).
Bonyolultabb van tranziensek reaktív elemek két lánc. Ebben az esetben, attól függően, hogy ezek a gyökerek a karakterisztikus egyenlet vagy aperiodikus vagy oszcilláló. Például, abban az esetben a soros csatlakozó elemek kell végezni, ha r> 2 arány
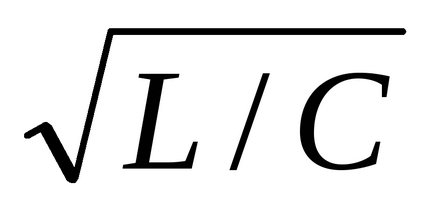
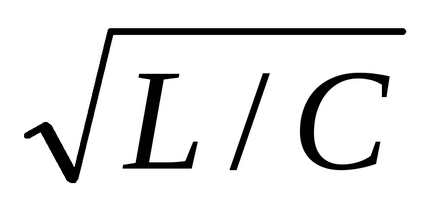
r = 2
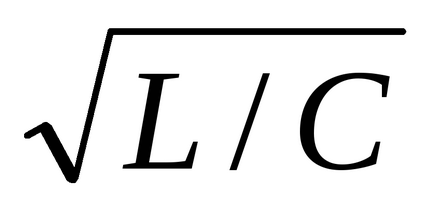
Amikor vibrációs folyamat értéke R / 2L jellemzi a sebességet a csillapítás folyamat, az állandó zatuhaniyaτ = 2L / r. A frekvencia így keletkező rezgések, meghatározva a kapcsolatban
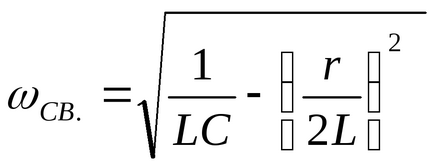
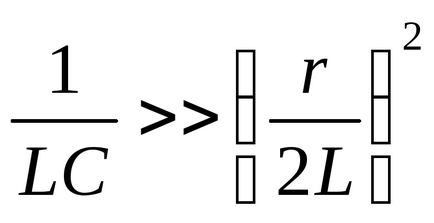
ωSV. ≈ω0 =