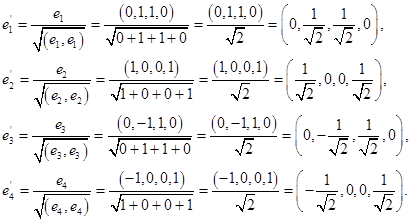Megállapító ortonormális alapján sajátvektorok egy szimmetrikus lineáris operátor,
Találunk sajátvektorok adott lineáris operátor.
A szám sajátértéke az üzemeltető akkor és csak akkor, ha. Írunk a karakterisztikus egyenlet:
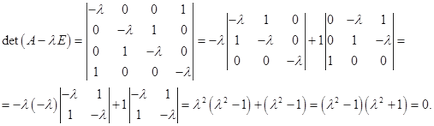
Megoldása, mi van
Így megkapjuk a sajátértékek:
Az egyes kapott sajátértékek találni sajátvektor.
Úgy megtalálja a rendszereket.
Mi megoldjuk a homogén egyenletrendszert.
Az együttható mátrix rangja 2. Kiválasztjuk az alapja kisebb Ezután feltéve, hogy van
Így, az általános megoldás a rendszer
.
A teljes megoldás találunk egy alapvető rendszer megoldások:
.
Használata alapvető megoldás a rendszer általános megoldást lehet írott formában.
Mi megoldjuk a homogén egyenletrendszert
.
Az együttható mátrix rangja 2. Kiválasztjuk az alapja kisebb Ezután feltéve, hogy van
Így, az általános megoldás a rendszer.
A teljes megoldás találunk egy alapvető rendszer megoldások:
.
Használata alapvető megoldás a rendszer általános megoldást felírható
.
Mi megoldjuk a homogén egyenletrendszert.
Az együttható mátrix rangja 4 mert
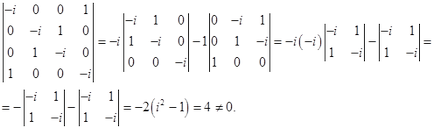
Mivel a rang megegyezik az ismeretlenek száma, a rendszer csak a triviális megoldás.
Mi megoldjuk a homogén egyenletrendszert.
Az együttható mátrix rangja 4 mert
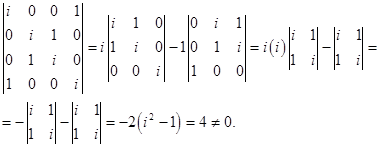
Mivel a rang megegyezik az ismeretlenek száma, a rendszer csak a triviális megoldás.
Így van saját vektor.
Úgy döntünk, mint ortogonális bázisa vektorok ,,,.
Normalizáld talált ortogonális bázisa: