1. ülés
Kör. alapvető meghatározások és képletek:
Ha a pont - egy tetszőleges pont a síkban, és a pont - fix pont, majd a =. Aztán - vektor formában a kör sugara. koordináta formájában kör egyenlete adja meg:
Ha az a kör közepén található az origó (0,0), a (1) egyenlet úgy a legegyszerűbb: → kanonikus egyenlete.
Ha kifejezés helyett (1) van egyenlőséget. könnyű megszerezni a kifejezést.
Attól függően, hogy az E értékét lehet megvalósítani ilyen esetekben:
. 1)> 0, akkor ott → kör :.
2). = 0 →. Ez végre egy ponton (x0, y0).
3). <0. то есть → – мнимая окружность .
1. példa -242. Hagyja, - a központ a kör - a kör sugara. . . - pont a kör. Az egyenlet a kör minden a következő esetekben:
1) (2, -3) = 7; 2) (2,6), (-1,2); 3) (3.2) (-1.6) - a végén a kör átmérője; 4) (1, -1), az egyenes vonal. = 0 kör érintője; 5) (1,2) - a kör pont az érintő a koordináta-tengely; 6) (3,1), (-1,3) - kerületi pont tartozik vonalon. = 0; 7) (-1,3), (0,2), (1, -1) - pont köre.
1). Most írunk az egyenlet a kör :.
2). A feltétel van: = = (2,6) - (- 1,2) = (3,4) → = = 5. Ekkor az egyenlet a kör :.
3). Mivel a központ a kör osztja a meghatározott hosszúságú félbe, majd =. ahol: 2 = + = (2,8) → = (1,4). Ugyanakkor = (- 4, -4) → = 2. Ekkor az egyenlet a kör :.
4). A kör sugara a távolság az érintési. Normalizálására egyenlet egy egyenes vonal, és megtalálni azt a pontot az eltérés ettől az egyenes: = 2 → = 2. Ezután - a kör egyenlete.
5). Legyen sugár = kerülete. Figyelembe véve az ingatlan érintési kerületi tengelyek, írhatunk egyenlet a kör :. Mivel a pont tartozik a kör, akkor van szükség :. Egyenlet ad két gyökér: = 1 = 5. Megoldás: vagy.
6). Pontok (3,1) és (-1,3) elszigetelt akkord a kör. Ismert tétel, hogy egy egyenes vonal. közepén áthaladó a húrt a kör és a rá merőleges, akkor átmegy a közepén a kör.
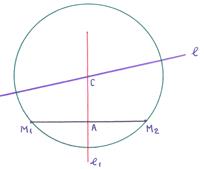
A metszéspont egyenes vonalak és talált következő egyenletek: megtaláljuk a középpontjának koordinátáit (2,4). Sugár: = = =. Ezután - az egyenlet a szükséges kerülete.
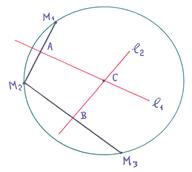
Keressük az egyenletet. A egyenlőségét vektorok a = 2 =. Találunk. Írunk =. fogadja = (1, -3). Ezután az egyenletet. . vagy.
A metszéspontja egyenes vonalak és megtalálják az egyenletrendszert: → (-4, -1). Sugár: = = = 5. Ezután - az egyenlet a szükséges kerülete.
Ellipszis. locus síkban, amelyek mindegyike a távolságok összege a két sík adatpontok nevű gócok. egy állandó, nagy. mint a távolság a foci.
Ha elfogadjuk, hogy - félig-nagytengely, a gócok az ellipszis található a tengelyen. És: = - bal fókusz = - jobb fókusz.
Canonical egyenlet egy ellipszis :. - semi-nagytengely - kisebb tengely. Value. . kapcsolatos a következő képlet: = -.
Egy fontos jellemzője az ellipszis az az érték: - az excentricitása amely meghatározza az összenyomódás mértékét mentén körbefutó tengely.
A távolság kiszámításához, hogy a hangsúly a kifejezést: =. =. Továbbá + = 2.
Egy különleges hely a tulajdonságok az ellipszis tart egy egyenes vonal, és - az igazgatónő. Igazgatónő helyzete határozza meg a számát :. A teljes szám a ellipszis:
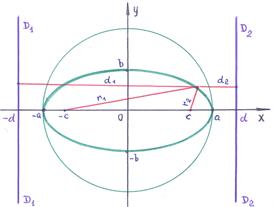
2. példa -249. Megállapítani, hogy az egyenlet b). ellipszis. Megtalálja a központ. félegyenes és igazgatónő az egyenlet.
1). Átírjuk az adott egyenlet :. vagy - a kanonikus egyenlete ellipszis a központ.
2). Tengely az ellipszis: = 5 = 4. Kiszámítjuk: = - = 9. Kiszámítjuk az excentricitás: =. A paramétereket a igazgatónő: =. Egyenletek igazgatónő. = -. . = Or. és. .
Válasz: b) center; ellipszisféltengelyek = 5 = 4; igazgatónő. . . .
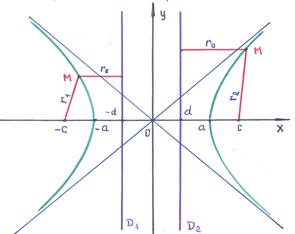
Hagyja túlzó gócok vannak tengelyén helyezkedik el. És: = - bal fókusz = - jobb fókusz. Canonical egyenlet a hiperbola van :. ráadásul <и . Эксцентриситет гиперболы: . Фокальные расстояния определяются выражениями:
Igazgatónő túlzó és adja meg a paramétereket. Aszimptota túlzás határozza meg a kifejezést: = ±.
Megjegyzés. A gócok tengely kapott nevezett helyen valós tengelye a hiperbola, a tengely - a képzetes tengelynek.
3. példa -265. Mivel az egyenlet a másodrendű sorban :. Mutassuk meg, hogy a vonal egy túlzás, hogy rögzítse a kanonikus egyenlete. Find: a) a fele-tengelyen, b) a koordinátákat a gócok, c) az excentricitást, z) a directrices és aszimptotákkal.
1). Átírni - a kanonikus egyenlete hiperbola tengelyén helyezkedik el.
2). Ellipszisféltengelyek hiperbola: = 3 = 4. Kiszámítjuk: = + = 25. Azaz: = - bal fókusz = - jobb fókusz. Kiszámítjuk az excentricitás: =. A paramétereket a igazgatónő: =. Egyenletek igazgatónő. = -. . =. Egyenletek aszimptotákkal expressziós: = ± = ±.
Válasz: a) az egyenlet a hiperbola. = 3 = 4; b) Focus =. =; c) = excentricitás; g) direktrixszel. = -. . =. asymptote: = ±.
4. példa -269 b). Mivel az egyenlet a másodrendű sorban :. Mutassuk meg, hogy a vonal túlzás, talált rá központ és rögzíti a kanonikus egyenlete. Keresés: fél-koordinátákat a gócok, különcség, egyenlet igazgatónő és aszimptotákkal.
1). Rewrite egyenlet: - egy kanonikus egyenlete hiperbola elrendezve egy egyenes vonal = 1, a központ (-5.1).
2). Mi használjuk a párhuzamos fordítást a koordinátarendszer :. . Ezután az egyenletet úgy kanonikus alakban, melyek minden érték lehet írni egy egyszerű képlet. Ellipszisféltengelyek hiperbola = 8 = 6. Számított: = + = 100. Azaz: = - bal fókusz = - jobb fókusz. Kiszámítjuk az excentricitás: =. A paramétereket a igazgatónő: =. Egyenletek igazgatónő. = -. . =. Egyenletek aszimptotákkal expressziós: = ± = ±.
3). Figyelembe véve. . Írunk az egyenleteket a régi koordináta rendszerben az igazgatónő. = -. . És aszimptotákkal = -1 = ±. Foci: =. =.
Válasz: Az egyenlet. = 8 = 6; Focus =. =; = Excentricitás; igazgatónő. = -. . =. asymptote: -1 = ±.
Parabola. pontok helye a síkban, amelyek mindegyikére a távolság egy előre meghatározott ponton a gép, az úgynevezett fókuszpont. egyenlő távolságra az előre meghatározott egyenes vonal, az úgynevezett direktrix.
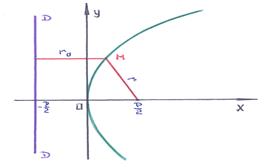
Az elfogadott a szám megjelölése szerint az elfogadott definíciója egy parabola. könnyű, hogy a kanonikus egyenlete parabola. Egy parabola: -ekstsentrisitet.
Megjegyzés. minta és helyét direktrix és a fókusz megfelelnek az az eset, amikor a parabola és a tengely a tengelyen.
1). Az egyenlet következik, hogy a tengelye a parabola. it = paramétert. parabola ága irányítani a megfelelő.
2). Az egyenlet következik, hogy a tengelye a parabola. Van egy parabola paraméter =. parabola ága felfelé irányuljon.
3). Az egyenlet következik, hogy a tengelye a parabola. Van egy parabola paraméter értéke 2, a menetrend adott parabola - grafikonja egy parabola. leképezett szimmetrikusan tengelyéhez képest. parabola ága irányítani a bal oldalon.
4). Az egyenlet következik, hogy a tengelye a parabola. Van egy parabola paraméter =. És a grafikon az adott parabola - grafikonja egy parabola. leképezett szimmetrikusan tengelyéhez képest. parabola ágai lefelé irányulnak.
6. példa -288. Annak megállapítására, hogy az egyes adott egyenlet: 1); 2); 3) határozza meg a parabola. Keresse meg a csúcsainak koordinátáit és a paraméter az egyes parabola.
1). Az egyenlet következik, hogy a tengelye a parabola. Van egy parabola paraméter =. parabola ágai lefelé irányulnak. Ütemezése meghatározott parabola - grafikonja parabola. kificamodott akár 2: van.
2). Az egyenlet következik, hogy a tengelye a parabola. Van egy parabola egy paraméter értéke 3, az ágakat a parabola lefelé. Ütemezése meghatározott parabola - grafikonja parabola. jobbra eltolt és le 6-1: van.
3). Az egyenlet következik, hogy a tengelye a parabola. Van egy parabola paraméter =. parabola ága irányítani a bal oldalon. Ütemezése meghatározott parabola - grafikonja parabola. a kiszorított balra 4 és legfeljebb 3: van.