Torzítatlan becslését variancia képlet határozza meg
Annak meghatározására statisztikai elvárás M * és D * statisztikai eltérés a véletlen változó X. építsünk egy hisztogram a statisztikai sokaság.
Határozat. A folyamatos eloszlása jellemző teljes tartományban, amelyben vannak zárva az összes megfigyelt értékek vonás van osztva több részleges időközönként h hosszúságú, és megállapította km - összeg gyakorisága változatok tartozó i-edik intervallumban. Hisztogram frekvenciákat az úgynevezett lépcsőzött kialakítású, álló téglalap, amelynek bázisok időközönként H hosszúságú. és a magassága arány egyenlő a mérföld / h (frekvencia sűrűség).
A területet a hisztogram frekvenciák összegével egyenlő az összes frekvenciát, azaz A minta térfogata. Keresek gyakorisági hisztogramot ábrán látható. 14.
Elfogulatlan becslések M * és D * jelentése találják, közép-vevő időközönként lehetőségek:
M * = (-450) · 0,01 + (-350) · 0,03 + (-250) · 0,07 + (-150) · 0,14 + (-50) · 0,25 + 50 · 0,24 +
+ 150 + 250 · 0,15 · 0,08 + 350 · 0,02 + 450 · 0,01 = 0.
Becslése a standard eltérést
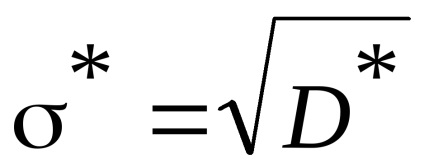
Értékelése az ismeretlen paraméter a lakosság egyetlen számot hívják pont becslést.
Együtt pontbecsléseket létezik intervallumbecslését, amikor a minta adatok épített numerikus tartomány, amelyre vonatkozóan az előre kiválasztott valószínűségi lehet mondani, hogy a becsült paraméter ebben az intervallumban. Intervallumbecslését különösen szükséges egy kis elemszáma, ahol a becsült pont nagyrészt véletlen, ezért kevés a megbízható.
6.7. Find konfidenciaintervallum becslések bizalommal valószínűsége 0,95 ismeretlen elvárás egy normál eloszlású jellemző X általános népességben, ha az adott általános szórása σ = 5, a minta azt jelenti, a * = 14 és n = 25 a minta térfogata.
Határozat. Annak megállapításához, a helymeghatározás pontossága a * matematikai statisztika megbízhatósági határokat és hogy meghatározzák a megbízhatóság - megbízhatósági valószínűsége. Trust hívás időtartam, amely egy előre meghatározott megbízhatósági β lefedi a becsült paraméter.
Annak a valószínűsége, sűrűsége normális eloszlású valószínűségi változó a következő formában:
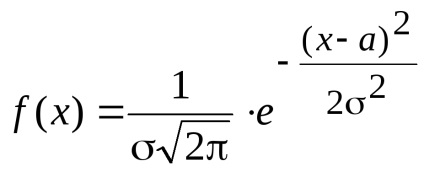
ahol - szórás, és - elvárás.
Ahhoz, hogy megbecsüljük a várható normális eloszlású X valószínűségi változó, átlagosan * mintát egy ismert szórása σ a teljes népesség szolgál megbízhatósági intervallum
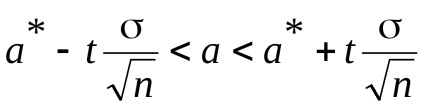
ahol
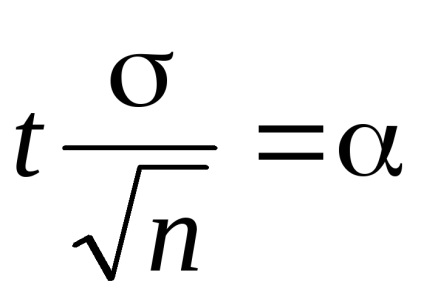
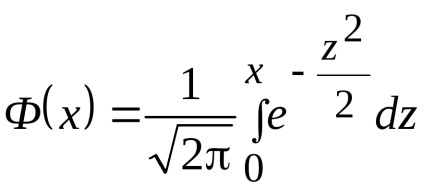
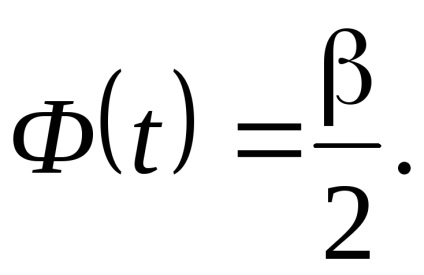
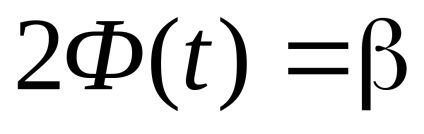
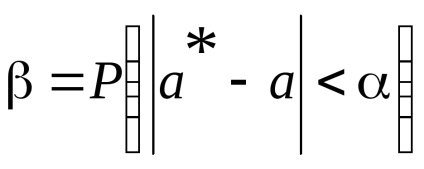
Találunk egy megbízhatósági intervallum (a * - α, a * + α). Erre találunk t. a kapcsolat