Számok ábrázolása a számítógépben 1
Számok ábrázolása a számítógépben
A számszerű adatok feldolgozása egy számítógép bináris jelölés. A számok a memóriában tárolt bináris kód, azaz a. E. sorozata nullák, és be lehet mutatni ebben a formában egy rögzített vagy lebegőpontos szám.
Egész számok a memóriában tárolódnak a fixpontos formátumban. Az ilyen formátum tárolására ábrázolásai szám nemnegatív egészek rendelt memória regiszter beleértve a nyolc memória sejtek (8 bit). Minden kategóriában megfelel a memória cella mindig azonos számú mentesítés, és rögtön a vessző LSB és kisülés rács. Például, a szám 11001101 tárolva van a regiszter memóriában az alábbiak szerint:
A maximális érték egy nem negatív egész, amely tárolható egy regiszterben a formában egy fix pont lehet meghatározni a következő képlet: 2 - 1, ahol n - a számjegyek száma a szám. A maximális száma ebben az esetben egyenlő 2 - 1 = 255 = 0 perc 11111111i = 00000000. Így a tartomány a nem negatív egész lesz a tartományban 0-255.
Ezzel szemben a tízes számrendszerben a számrendszer egy számítógépes reprezentációja bináris számot nem szimbólumokat, hogy képviselje a jele száma: pozitív (+) és negatív (-), tehát, hogy képviselje aláírt egész bináris rendszer két formátumot szám: a méret értékének aláírt és kiegészítő kód formátumban. Az első esetben tárolására aláírt egészek hozzárendelt két memória regiszterek (16 bit), az MSB (balra) mellett használják a jele a számot, ha az pozitív, az előjelbit 0 van írva, ha a szám negatív, akkor - 1. példa száma 536 = 0000001000011000budet képviselt a memóriában regisztrálja a következőképpen:
egy negatív szám -536 = 1000001000011000 formájában:
A maximális számát pozitív vagy negatív minimum értéket a formátumát számok (összefüggésben a kisülési jel alatt) 2 - 1 = 2 - 1 = 2 - 1 = 32767 = 111111111111111 és a számtartományt lesz a tartományban -32.767-32.767.
Leggyakrabban képviselni aláírt egész bináris rendszerben alkalmazandó kiegészítő kód formátumban, amely lehetővé teszi, hogy cserélje ki egy aritmetikai kivonási művelet a számítógépes műveletek mellett, ami nagyban leegyszerűsíti a szerkezet a mikroprocesszor és növeli a sebességet.
Ahhoz, hogy képviselje a negatív egész szám formátumban által használt egy további kódot, amely képviseli a összeadó egység egy negatív szám nullára. Fordítása az egész negatív számot a kiegészítő kód végzi a következő műveleteket:
1) közvetlen írási kód modullal a n (n = 16) bitet;
2), hogy megkapja a visszatérési kódját (az a szám, hogy fordítsa az összes bit, azaz az összes egység helyett nullák, és nullák - egységre) ..;
3) a kapott inverz kódot hozzá egy-LSB.
Például száma -536 ebben a formátumban a modul lesz egyenlő 0000001000011000 inverz kód - 1111110111100111, és a kiegészítő kód - 1111110111101000. ellenőrizni kiegészítő kód értéket kapunk a számológép. Ehhez adjon meg egy értéket -536 modul, azaz a. E. száma 536, és az opcionális Bin gombot, átalakítani ezt a számot képviseli tízes számrendszerben, a bináris rendszer telepítése után a választható gombot 2 bájt. Nem nyomja a számológép gombbal lépjen vissza a kódszámot, és hozzátéve, hogy az ellenkező bináris kód egység - kiegészítő kódot. A végső eredményt kaptuk Field kalkulátor ablakban (ábra. 2.6). Meg tudod csinálni még egyszerűbb: gépelni egy számológép száma -536i aktiváló Bin gombot. minél több kódot ezt a számot a bináris rendszer.
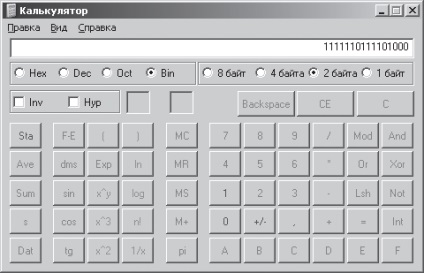
Ábra. 2.6. Eredmény pótlólagos kód
Emlékeztetni kell arra, hogy a kiegészítő kód pozitív szám - magát a számot.
Tárolni aláírt egész amellett, hogy 16 bites számítási teljesítmény, ha két memória regiszterek (ez a szám formátum is nevezik a rövid formátumban egész számok előjellel), alkalmazva formátumok a közép- és hosszú aláírt egészek. A számok ábrázolása ebben a formában átlagok használt négy regiszterek (4 x 8 = 32 bit), és a számok ábrázolása ebben a formában a hosszú egész - nyolc regiszterek (8 x 8 = 64 bit). A értéktartományait a mérete közepes és hosszú számok rendre egyenlő: - (2 - 1) ... + 2 - 1, és - (2-1) ... + 2 - 1.
Számítógépes számok ábrázolása a fix pont méret megvannak a maga előnyei és hátrányai. Az előnyök közé tartozik a könnyű számok ábrázolása és algoritmusok végrehajtására vonatkozó aritmetikai műveletek, a hiányosságokat - a végső képviseletét a különböző számok, hogy nem lehet elég, hogy megoldja számos gyakorlati problémát (matematikai, gazdasági, fizikai, stb ...).
Valós számok (véges és végtelen tizedes) feldolgozzák és tárolják a számítógép lebegőpontos formátumban. Ezzel a megjelenési formája a tizedes pont a felvételi változhat. Bármely valós szám Rk lebegőpontos formátum is képviselteti magát:
ahol A - több mantissza; h - radix; p - a megrendelés számát.
A kifejezés (2.7) a tízes számrendszerben formáját ölti:
Ez a fajta ábrázolás számát is nevezik normális. A változás az, hogy a vessző a műszakok száma, azaz a. E. Mivel úszik balra vagy jobbra. Ezért a normál forma számok ábrázolása az úgynevezett forma lebegőpontos. Decimális 15,5, például egy lebegőpontos formátum lehet reprezentálni: 0,155 · 10; 1,55 · 10; 15,5 · 10; 155,0 · 10; 1550,0 · t és a 10. D. Ez a jelölés 15,5 decimális lebegőpontos nem írásához használt számítógépes programok, valamint bemenet őket a számítógépre (számítógépes beviteli eszközök érzékelik csak a lineáris adatrögzítés). Ennek alapján ez a kifejezés (2.7) decimális számok és bemeneti őket egy számítógépre, hogy átalakítsa az elme
ahol F - a tételszám,
.. Azaz ahelyett, radix 10 a levelet E rendszer helyett a tizedes pont - a pont, majd megszorozzuk a megjelölés nincs hozzárendelve. Így a száma 15,5 lebegőpontos formátumban, és a felvételt a lineáris (számítógépes reprezentáció) lesz írva formájában: 0.155E2; 1.55E1; 15.5E0; 155.0E-1; 1550.0E-2, stb
Tekintet nélkül a rendszer formájában bármennyi lebegőpontos leírható egy végtelen számsor. Ez a fajta írás az úgynevezett non-normalizálódott. Mert egyértelmű ábrázolása lebegőpontos számok segítségével normalizált formában rekordszámú, amelynél a száma mantissza kell felelnie állapot
ahol | A | - az abszolút értéke a mantissza.
Állapot (2.9) azt jelenti, hogy a mantissza rendben kell lennie, és egy lövés után a decimális szám, amely különbözik a nullától, vagy más szóval, ha a tizedesvessző után a mantissza nem nulla, akkor a számot hívják normalizálódott. Így a száma 15,5 normalizált formában (normált mantissza) formájában lebegőpontos az alábbiak lesznek: .. 0,155 · 10, azaz normált mantissza lesz = 0155 és sorrendben P = 2, vagy a számítógépes ábrázolása száma 0.155E2 .
A számok lebegőpontos formában van egy fix méret és a számítógép memóriájában foglalnak négy (32 bit) vagy nyolc byte (64 bit). Ha ez a szám megy a számítógép 32 bites memória, ez az a szám, egyszeres pontosságú, ha 64 bites, ez a dupla pontosságú szám. Amikor a felvétel száma lebegőpontos bitet rendelünk tárolására a mantissza jel, a jel a sorrendben, és az, hogy a mantissza. A bitek száma, amely által a megrendelés számát, körét, a változás a számok, és a hozzárendelt bitek számának tárolására mantissza - a pontosság, amellyel a megadott számot.
Ha az aritmetikai műveletek (összeadás és kivonás) a szám képviseli lebegőpontos formátum, végre a következő eljárást (algoritmust):
1) fedésben vannak érdekében, számokat, amelyek az aritmetikai műveleteket végeznek (eljárás kisebb modulo szám növekszik magasabb értékre érdekében modulo száma, a mantissza csökken az ugyanannyi idő alatt);
2) aritmetikai műveletek végrehajtását mantisszákra számok;
3) a normalizáció az eredmény végezzük.
Hadd illusztráljam a fenti példákkal.
Elvégezzük a két új szám 0,5 és 0,8 · 10 · 10 a lebegőpontos formátum.
Döntetlen összehangolás megrendelések mantisszák és a hozzáadott 0,05 x 10 + 0,8 * 10 = 0,85 * 10 0,85 A kapott mantissza normalizáltuk, mivel megfelel állapotban (2.9).
Elvégezzük a két új szám 0,1 és 0,1 · 2 · 2 lebegőpontos formátumban.
Döntetlen összehangolás megrendelések és mantisszák hozzáadása: 0,01 · 2 + 2 = 0,1 · 0,11 · 0,11 2. A kapott mantissza normalizáltuk, mivel megfelel állapotban (2.9).