sebesség mátrix
Definíció. Lépés lesz úgynevezett mátrix, amely a következő tulajdonságokkal rendelkezik:
1) ha az i-edik sorban nulla, akkor (i + 1) edik sorban is nulla,
2) ha az első nem nulla elemei az i-edik és (i + 1) -edik sorok vannak elrendezve oszlopok indexek k és R, illetve a K Feltételek 2) előírja kötelező növekedése nullákat maradt az átmenetet a i-edik sorának az (i + 1) -edik sor. Például, a mátrix lépcsőzött, és a mátrix Nem megtántorodott. 5.1 Tétel. Bármilyen mátrix vezethet lépésenként elemi transzformációs mátrix sorok. Hadd illusztráljam ezt a tételt egy példát. Az így kapott mátrixot # 9472; sebesség. Definíció. A helyezés egy mátrix, hogy a szám nem nulla sorok a lépcsős formájában a mátrix. Például, a rangot a mátrix az előző példa 3. Meghatározói és azok tulajdonságait. Inverz mátrix és annak kiszámítása. A másodlagos azonosító. Tekintsük a másodrendű négyzetes mátrix Definíció. másodrendű determinánsa megfelelő mátrix egy szám képlettel számítottuk ki Az elemek aij nevezzük elemei a meghatározó # 9474, A # 9474;, A11 elemek. A22 adják a fő átló. és az elemek a12. a21 # 9472; mellékes. Példa.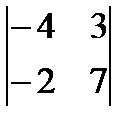
A meghatározó a harmadik rend.
Tekintsük a négyzetes mátrix a harmadik rend
Definíció. A meghatározója a harmadik rend, a megfelelő mátrix egy szám képlettel számítottuk ki
, Hogy melyik működik a jobb oldalon kell hozni egy „plusz”, és amely # 9472; A jel „mínusz”, érdemes emlékezni a szabály, amely az úgynevezett háromszög szabályt.
1)
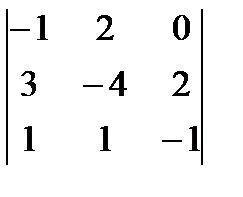
2)
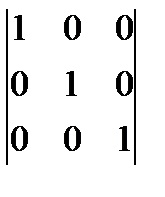
Vegyünk egy másik módja annak, hogy kiszámítja a meghatározója a harmadik rend.
Definíció. Kisebb elem aij determináns az a meghatározó nyert ezt törlési i-edik sorának és j-edik oszlop. A kofaktora aij meghatározó eleme Aij nevezzük annak csekély Mij. venni a megjelölés (-1) i + j.
Példa. Kiszámítjuk M23 Minor és kofaktorspecificitásuk A23 A23 elem a mátrix
Kiszámítjuk a Minor M23:
M23 =
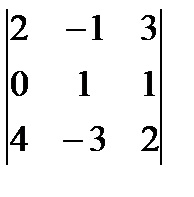
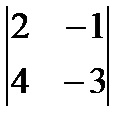
1. Tétel A determináns az összege a harmadik végzést termékei az elemek egy sor (oszlop) által kofaktorokat.
Bizonyítás. definíció szerint,
Válasszunk például a második sorban, és megtalálja kofaktor A21. A22. A23: