Megoldás összehasonlítása az első fokú
Összehasonlítás az első fokú egy ismeretlen van:
Problémák összehasonlítás - azt jelenti, hogy megtalálja az összes x értékei elégítette ki. Két összehasonlítást, amely eleget tesz az azonos x értékei nevezzük egyenértékű.
Ha az összehasonlítás (1) megfelel minden X = x1, majd (a 49), mint az azonos, és kielégíti az összes szám összehasonlítható x1. modulo m. x x1 (mod m). Ez az egész számcsalád számít az egyik megoldás. Ha egy ilyen megállapodást lehet következtetni, hogy.
66.Sravnenie (1) lesz annyi megoldás, mint a maradék a teljes rendszer megfelel neki.
6x - 4 0 (mod 8)
a számok között 0, 1,2, 3, 4, 5, 6, 7 komplett maradékot rendszer modulo 8 megfelelnek két szám: x = 2 és X = 6. Ezért, a fenti összehasonlítás két megoldást:
x 2 (mod 8), x 6 (mod 8).
Összehasonlítása az első fokú szabad átadása a tag (az ellenkező megjelölés), hogy a jobb oldalon, hogy a forma
Tekintsük a összehasonlítás megfelel (a. M) = 1.
66 szerint összehasonlítás annyi megoldás, mint a maradék a teljes rendszer megfelel neki. De amikor X végigfut egy teljes maradékot rendszer modulo m, majd ax fut keresztül a teljes rendszer a maradékok (60). Következésképpen, ha egy és csak egy x értékét, amelyet kivett a teljes rendszer összehasonlítható lesz ah b. Így
67. (a, m) = 1-összehasonlítás axb (mod m) van egy megoldás.
Most (a. M) = d> 1. Ekkor, az összehasonlítás (2) van egy megoldás, szükség van (55), hogy a B osztva d, máskülönben az összehasonlítás (2) lehetetlen bármilyen általános x. Feltételezve, azonban több b d, a = A1D. b = B1D. m = m1d. Ezután összehasonlítás (2) egyenértékű a következő (redukcióval d): a1xb1 (mod m), hogy a már (. A1 m1) = 1, és így arra is egy megoldás modulo m1. Hagyja x1 - a legkisebb nemnegatív maradéka ezt a megoldást modulo m1, akkor az összes szám x, alkotó megoldás, van egy
Modulo jelentése mchisla (3) formájában több mint egy oldatot, és pontosabban annyi megoldásokat, mint a számok (3) van egy száma 0, 1, 2 ,. m - 1 a legkisebb nem-negatív maradékok modulo m. De itt lesz a következő számokat (3):
azaz Összesen d számok (3); Ezért, az összehasonlítás (2) van egy D-készítés.
68. Let (a, m) = d. Összehasonlítás ax b (mod m) lehetetlen, ha b nem osztható d. Ha b, többszöröse d, d jelentése az összehasonlítás megoldások ..
69.Sposob megoldások összehasonlítjuk az első fokú, az elméleten alapul lánctörtekkel:
Bővítése egy frakció továbbra áttétel m: egy,
és figyelembe véve az elmúlt két convergents:
tulajdonságai szerint lánctörtekkel (szerinti 30), van
Így, az összehasonlítás van egy megoldás
a megállapítás, amely elegendő ahhoz, hogy kiszámításához Pn- 1 eljárás szerint ismertetett 30.
Példa. Mi megoldjuk összehasonlítás
111x = 75 (mod 321). (4)
Itt (111, 321) = 3, és 75 többszöröse 3. Ezért az összehasonlítást három megoldásokat.
Elosztjuk mindkét oldalán, és összehasonlító egység 3, akkor nyíljon
37x = 25 (mod 107) (5)
hogy meg kellene először megoldani. van
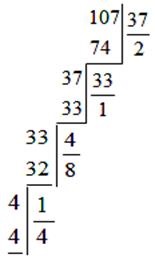
Ezért ebben az esetben n = 4, Pn-1 = 26, b = 25, van egy megoldás, és összehasonlítjuk (5) formájában
x -26 # 8729; 25 99 (mod 107).
Ebből az összehasonlításból (4) döntés a következő: A
x 99; 99 + 107; 99 + 2 # 8729; 107 (mod 321),
X º99; 206; 313 (mod 321).
Kiszámítása inverz elem egy adott modulusa
70.Esli egészek és n jelentése viszonylag elsődleges, létezik egy”. kielégítő, mint a # 8729; egy „≡ 1 (mod n). A szám egy „úgynevezett reciprok egy modulo n és egy kijelölés használt érte - 1 (mod n).
Számítása inverz értékek egyes modul lehet végezni összehasonlítjuk az első fokú egy ismeretlen oldat, ahol a számot egy „veszik, mint x.
Megoldást találni a kongruencia
Használhatja az euklideszi algoritmus (69) vagy a Fermat-tétel, Euler, amely kimondja, hogy ha (a, m) = 1, akkor
Csoportok és tulajdonságaik
Group - az egyik rendszertani osztályba alkalmazott osztályozási matematikai struktúrák közös jellemző tulajdonságait. Csoportok két részből áll: egy sor (G) és () meghatározott művelet ezen a beállított.
A fogalmak készletek, elemek és tartozékok alapvető meghatározatlan fogalmak a modern matematika. Bármilyen elemkészlet határozzuk, a hozzá tartozó (amely viszont, is lehet készletek). Így azt mondhatjuk, hogy a van meghatározva, vagy állítva, ha tudjuk megmondani, hogy ez az a készülék vagy nem tartozik bármely elemét.
Mert két A, B BA felvételt. BA. B ∩ A. BA. B \ A. A × B jelentése rendre B egy részhalmaza A (vagyis, minden eleme B tartalmazza továbbá A. például a természetes számok halmaza tartalmazza a valós számok halmaza, továbbá, mindig AA), B valódi részhalmaza a készlet egy (azaz, a BA és B ≠ a), a kereszteződésekben a halmazok B és a (vagyis, az összes elemet, hogy feküdjön mind A. és B. például kereszteződés egész számok, és a pozitív valós számok a természetes számok halmaza), a Union halmazok B és a (vagyis a beállított elemekből álló Amelyek ellen sem, vagy A. B), különbség meghatározza a B és A (vagyis, elemek sokaságát amelyek fekszenek a B. de nem fekszenek egy), Descartes-szorzat az A és B halmaz (azaz, több pár fajok (a. b), ahol aa. bB). Keresztül | A | Mindig azt jelezte, hogy a számossága A. az elemek száma a készletben A.
Működés - a szabály, amely szerint bármely két eleme a G (a és b) hozzá van rendelve egy harmadik eleme G: és b.
A több elem a nevezett művelet G sáv. ha az alábbi feltételek teljesülnek:
1. Az asszociatív. minden elem a, b, cG a egyenlőség (b c) = (a b) c.
2. Az elemi cella: van egy elem e G, hogy minden G egyenlőségek egy e = e a = a.
3. Fordított elem. mindegyik egy G létezik egy elem egy 'G. kielégíti azt a kapcsolatban a' = A „= A e.
Egy elem e G úgynevezett semleges eleme a csoport, és az elem egy „- inverz elem egy. A visszaállító elem jelöli a „= A - 1.
Csoportok kommutatív művelet. azaz bármely két a. b G egyenlősége egy b = b a. úgynevezett kommutatív csoportok vagy Abel-csoport.
A elemek száma a csoportban az úgynevezett annak érdekében.
Ami a megoldása az egyenleteket alapvető tulajdonsága a csoport, hogy egyértelműen lehetővé tette a típusú egyenletet:
minden a, b G.
1. Egész, racionális, valós, komplex számok alatt tartjuk.
2. A nem nulla racionális, valós, komplex számok alatt szorzás.
Mindezek a csoportok Abel.