Horner szabály
Horner szabály - egy eljárás elosztjuk a polinom
A binomiális $ x-egy $. Fog működni egy asztal, az első sor tartalmazza az együtthatók egy előre meghatározott polinom. Az első elem a második sor lesz a szám $ a $, kivenni a binomiális $ x-a $:
Miután a szétválás a polinom n-ed-fokú a binomiális $ x-a $, polinom, amelynek mértéke eggyel kevesebb, mint a kezdeti, azaz a egyenlő $ $ n-1. Közvetlen alkalmazását Horner rendszer legegyszerűbb megmutatni példákat.
Osszuk $ 5x ^ 4 + 5x ^ 3 + x ^ 2-11 $ a $ x-1 $, a Horner rendszer.
Készítsünk táblázatot két sor: egy első sort levelet polinom együtthatók $ 5x ^ 4 + 5x ^ 3 + x ^ 2-11 $, rendezve csökkenő fokban változó $ x $. Megjegyzendő, hogy a polinom nem tartalmaz $ x $ az első fokú, azaz a együtthatója az $ x $ az első fokú 0. Mivel osztunk $ x- $ 1, a második sorban olvasó egység:
Kezdjük, hogy töltse ki az üres cellák a második sorban. A második cella a második sor írási szám $ 5 $ áthelyezésével azt a megfelelő első sejtvonal:
Töltse ki a következő cellába a következő elv: $ 1 \ cdot 5 + 5 = 10 $:
Hasonlóképpen, töltse ki, és egy negyedik cella a második húr: $ 1 \ cdot 10 + $ 11 = 1:
Az ötödik cella kapjunk $ 1 \ cdot 11 + 0 = 11 $:
És végül, az utolsó, a hatodik cella, van $ 1 \ cdot 11 + (- 11) = $ 0:
A probléma megoldódott, már csak azt kell írni a választ:
Mint látható, száma, amelyek a második sorban (egytől nulla), vannak olyan polinom együtthatók után kapott elosztjuk $ 5x ^ 4 + 5x ^ 3 + x ^ 2-11 $ a $ x-1 $. Természetesen, mivel a foka az eredeti polinom $ 5x ^ 4 + 5x ^ 3 + x ^ 2-11 $ egyenlő négy, a mértéke a polinom kapott $ 5x ^ 3 + 10x ^ 2 + 11x + 11 $ kevesebb egységnyi, azaz . Ez egyenlő a három. Az utolsó szám a második sorban (nulla) azt jelenti, a fennmaradó részlege a polinom $ 5x ^ 4 + 5x ^ 3 + x ^ 2-11 $ a $ x-1 $. Ebben az esetben, a maradék zérus, vagyis polinomok egyenletesen elosztva. Ez az eredmény még mindig a következőkkel jellemezhető: a polinom értékét $ 5x ^ 4 + 5x ^ 3 + x ^ 2-11 $ a $ x = 1 $ nulla.
O, és formulázható formájában: a polinom értékét $ 5x ^ 4 + 5x ^ 3 + x ^ 2-11 $ a $ x = 1 $ nulla, a készülék egy gyökér a polinom $ 5x ^ 4 + 5x ^ 3 + x ^ 2-11 $.
Osszuk a polinom $ x ^ 4 + 3x ^ 3 + 4x ^ 2-5x-47 $ a $ x + $ 3 Horner rendszer.
Állapítani, hogy a kifejezést $ x + $ 3 kell képviselni formájában $ x - (- 3) $. A Horner rendszer vesz részt az $ -3 $. Mivel a mértéke az eredeti polinom $ x ^ 4 + 3x ^ 3 + 4x ^ 2-5x-négy egyenlő 47 $, az eredmény elosztjuk a polinom harmadik foka:
Ez az eredmény azt jelenti, hogy
$$ x ^ 4 + 3x ^ 3 + 4x ^ 2-5x-47 = (x + 3) (x ^ 3 + 0 \ cdot x ^ 2 + 4x-17) + 4 = (x + 3) (x ^ 3 + 4x-17) + 4 $$
Ebben a helyzetben, a maradék osztály $ x ^ 4 + 3x ^ 3 + 4x ^ 2-5x- $ 47 és $ x + 3 egyenlő $ $ 4 $. Vagy, ami ugyanaz, a polinom értékét $ x ^ 4 + 3x ^ 3 + 4x ^ 2-5x-47 at $ $ x = -3 $ értéke $ 4 $. By the way, ez könnyen kettős ellenőrzés közvetlen helyettesítés $ x = -3 $ egy adott polinom:
$$ x ^ 4 + 3x ^ 3 + 4x ^ 2-5x-47 = (- 3) ^ 4 + 3 \ cdot (-3) ^ 3-5 \ cdot (-3) -47 = 4 $$.
Ie Horner szabály is alkalmazható, ha szükséges megtalálni a polinom értékét egy adott változó értékét. Ha a cél -, hogy megtalálja a gyökereit egy polinom, a Horner rendszert lehet alkalmazni egymás után többször - mindaddig, amíg nem fogy el az összes gyökerek, a tárgyalt példában №3.
Find összes egész gyökerei a polinom $ x ^ 6 + 2x ^ 5-21x ^ 4-20x ^ 3 + 71x ^ 2 + 114X + $ 45, a Horner rendszer.
A polinom együtthatóit tekinthető egész számok, és az együttható a legmagasabb fokozatot a változó (azaz, mielőtt a $ x ^ 6 $) egyenlő egységét. Ebben az esetben az egész gyökerei a polinom kell törekedni között szabad tagjai osztók, azaz között osztója 45. Egy adott polinom gyökerek ilyen lehet több 45 $; \; 15; \; 9; \; 5; \; 3; \; $ 1 és $ -45; \; -15; \; -9; \; -5; \; -3; \; -1 $. Ellenőrizzük, például, hogy hány $ 1 $:
Mint látható, a polinom értékét $ x ^ 6 + 2x ^ 5-21x ^ 4-20x ^ 3 + 71x ^ 2 + 114X + $ 45 a $ x = 1 egyenlő $ $ $ 192 (az utolsó szám a második sorban), ahelyett, $ 0 $, így a készülék nem gyökér e polinom. Mivel a csekket az egység volt sikertelen, ellenőrizze a $ x = -1 $. Új tábla erre nem lesz, és továbbra is használni asztalra. №1, miután hozzá egy új (harmadik) vonal. Második sor, amely ellenőrzi az értéke $ 1 $, pirossal kiemelt, és az azt követő beszélgetés nem fogjuk használni.
Akkor, persze, csak átírni az asztal újra, de feltöltése manuálisan időt vesz igénybe. Különösen azért, mert a számok, ellenőrzését, amely sikertelen lesz, lehet, hogy több, és minden alkalommal, hogy rögzítse új tábla nehéz. Kiszámításakor az „papíron” vörös vonalat lehet egyszerűen eltávolítottak.
Így a polinom értékét $ x ^ 6 + 2x ^ 5-21x ^ 4-20x ^ 3 + 71x ^ 2 + 114X + $ 45-on $ x = -1 $ nulla, azaz a szám $ -1 $ egy gyökér e polinom. Miután a szétválás a polinom $ x ^ 6 + 2x ^ 5-21x ^ 4-20x ^ 3 + 71x ^ 2 + 114X + $ 45 a bab $ x - (- 1) = x + 1 $ kap a polinom $ x ^ 5 + x ^ 4-22x ^ 3 + 2x ^ 2 + 69x + $ 45, amelynek együtthatókat venni a harmadik sorban a táblázatban. №2 (lásd. Példa №1). A számítás eredményét is leírható a következő formában:
Továbbra is keresni egész gyöke. Most meg kell keresni a gyökereit polinom $ x ^ 5 + x ^ 4-22x ^ 3 + 2x ^ 2 + 69x + 45 $. Ismét, az egész gyökerei a polinom keres között osztói annak abszolút kifejezés - száma $ 45 $. Próbáljuk még egyszer ellenőrizze a számot $ -1 $. Az új tábla nem lesz, és továbbra is használja az előző táblázatban. №2, azaz Töltse ki egy másik vonal:
Így a száma $ $ -1 egy gyökér a polinom $ x ^ 5 + x ^ 4-22x ^ 3 + 2x ^ 2 + 69x + $ 45. Ez az eredmény felírható:
Figyelembe véve egyenlet (2), a (1) egyenlet átírható formájában:
Most meg kell keresni a gyökereit a polinom $ x ^ 4-22x ^ 2 + 24x + $ 45, - természetesen között osztó abszolút kifejezés ($ number $ 45). Ellenőrizze újra a számot $ -1 $:

A szám $ -1 $ egy gyökere $ x ^ 4-22x ^ 2 + 24x + $ 45. Ez az eredmény felírható:
Tekintettel egyenlet (4), (3) egyenlet átírható formájában:
Mi most keresi a gyökereit a polinom $ x ^ 3-x ^ 2-21x + 45 $. Ellenőrizze újra a számot $ -1 $:

Az ellenőrzés sikertelen. Hatodik sor megkülönböztetni a vörös és megpróbálja ellenőrizni egy másik számot, például, hogy hány $ 3 $:

A egyenlege nulla, ezért a számot $ 3 $ - figyelembe vette a gyökér a polinom. Tehát, $ x ^ 3-x ^ 2-21x + 45 = (X-3) (x ^ 2 + 2x-15) $. Most a (5) egyenlet átírható, mint:
Nézzük meg újra a számot $ 3 $:

Ez az eredmény felírható (folytatása (6) egyenlet):
Az utolsó zárójelben látható, hogy a szám $ -5 $ is gyökere a polinom. Akkor, persze, technikailag továbbra Horner rendszer ellenőrzi az értéke $ x = -5 $, de ez nem feltétlenül szükséges. Így
A több $ 1; \; 3; \; 5 $ - a gyökerei a polinom. Továbbá, mivel a konzol $ (x + 1) $ a harmadik fokozatot, a $ -1 $ - a gyökér a harmadik sorrendben; mivel a keretet $ (X-3) $ a második fokozatot, a $ 3 $ - a gyökér a másodrendű; mivel a keretet $ (X + 5) $ az első fokú, a $ x = -5 $ - a gyökér az elsőrendű (egyetlen gyökér).
Általában, a szokásos tervezési ilyen példa tartalmaz egy táblázatot, amelyben az opciók mozognak a gyökereket, és a válaszokat:
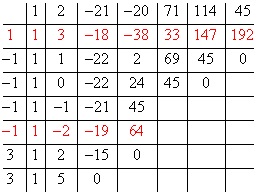
A táblázat alapján megállapítható, hogy mi korábban kapott részletes megoldások:
Ellenőrizzük, hogy a száma $ 2 és $ $ $ -5 a gyökerek a polinom $ 3x ^ 6 + 9x ^ 5-28x ^ 4 + 6x ^ 3-30x ^ 2-30x + 100 $. Osszuk az adott polinom x-binomials $ 2 $, és $ x + $ 5.
A polinom fokának $ 3x ^ 6 + 9x ^ 5-28x ^ 4 + 6x ^ 3-30x ^ 2-30x + 100 a $ $ $ 6. Miután elosztjuk két, előre meghatározott binomiális előre meghatározott mértékben polinom csökkenést $ 2 $, azaz a Ez egyenlő lesz $ 4 $.
Természetesen ez a kiválasztási módszer nem nagyon hatékony az általános esetben, amikor a gyökerek nem egész számok, hanem egész gyöke a módszer meglehetősen jó.