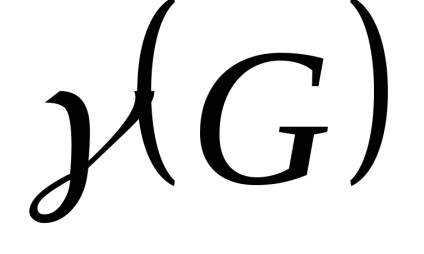Előadás № 4 színezés

1. Bevezetés

A különböző problémák a termelés tervezése, előkészítése az ellenőrzési ütemterv, tárolása és szállítása az áruk, stb Ez gyakran jelenik meg problémaként gráfelmélet, amely szorosan kapcsolódik az úgynevezett „munka színezés.” Grafikonok ebben a fejezetben tárgyaljuk nem orientált, és nem alkotja; Hacsak kifejezetten másként, a „grafikon” kifejezés pontosan ezt a grafikonon.

gróf

r-kromatikus ha csúcsai mogutbyt festett r segítségével színek (festékek), úgy, hogy nincs két szomszédos csúcsa azonos színű. A legkisebb szám r. úgy, hogy G jelentése r- kromatikus az úgynevezett kromatikus száma G és jelöljük . A probléma a megállapítás a kromatikus száma a grafikon nevezzük a problémát a színező (vagy színező objektum) a grafikon. Ennek megfelelő csúcsok száma színező osztja a csúcsok halmaza a r részhalmazait, amelyek mindegyike tartalmazza a csúcsok az azonos színű. Ezek a készletek függetlenek, hiszen egy sor belül nincs két szomszédos csúcsot.

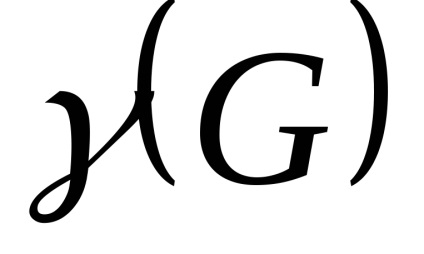
Általánosságban elmondható, hogy a kromatikus száma grafikon (valamint a több függetlenséget és az uralom, tárgyalt az előző fejezetben) nem található, jóllehet csak a csúcsok száma és élek a grafikonon. Nem elég, hogy jól ismerik a minden csúcsa kiszámításához kromatikus száma a grafikonon. Ez látható figyelembe véve a grafikonok az 1. ábrán látható (a) és az 1. ábra (b). Ezeket a grafikonokat az n = 12 csúcsa, m = 16, a bordák és az azonos eloszlása ​​fokú csúcsok

. Azonban, a kromatikus száma grafikonjait adatai megegyeznek a 4 és 2 ill. Az ismert értéke n (csúcsok száma), m (élek számát), és (Fok csúcsok) lehet a felső és alsó határ a kromatikus számát egy grafikon. Becslések a következő részben.

A probléma megtalálni a kromatikus száma egy tetszőleges gráf tárgyát képezte számos tanulmány és a végén XIX az aktuális században. Most a témában ismert, hogy számos érdekes eredményt. Ebben a fejezetben azonban nem próbálunk beszélni ezeket az eredményeket, vagy legalábbis nekik egy rövid áttekintést. Bemutatjuk csak azokat a fogalmakat, amelyek szükségesek építésére algoritmusok a probléma megoldásának gráfszınezés. Itt tartjuk az alapvető algoritmusok (mind a pontos és a „közelítő”), amely lehetővé teszi számunkra, hogy megtaláljuk (pontos vagy hozzávetőleges érték) a kromatikus száma tetszőleges gráf és a megfelelő csúcs értéke színezés.

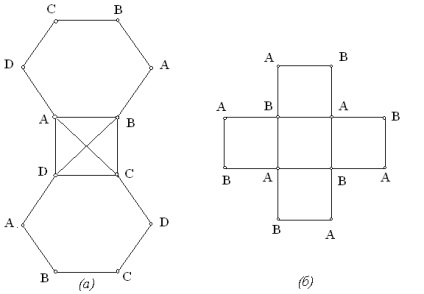
1. ábra. Két grafikon az azonos n, m és a forgalmazási a fokú csúcsok, de eltérő a kromatikus szám. (A)

.(B) .

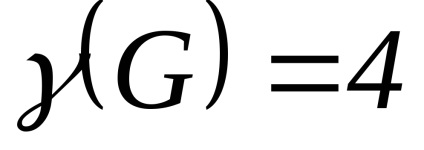
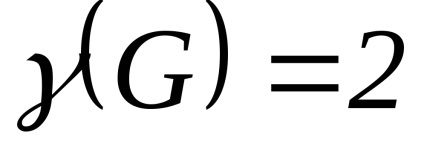
2. Egyes tételek és becslések kapcsolódó kromatikus számának

2.1. Alsó korlátot.

Mivel az alkalmazottak száma

egyenlő a legnagyobb teljesítmény mnozhestvapoparno nem szomszédos csúcsai G. is egybeesik a maximális kapacitása a több csúcsot a G, amely lehet azonos színű, és ezért,

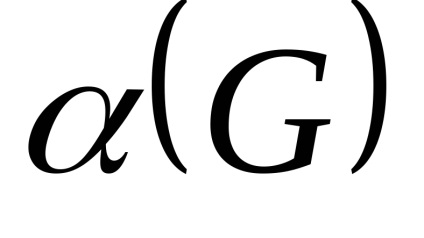
ahol n - a csúcsok száma és G.

jelöli naibolsheetseloe száma nem haladja meg a számot x.

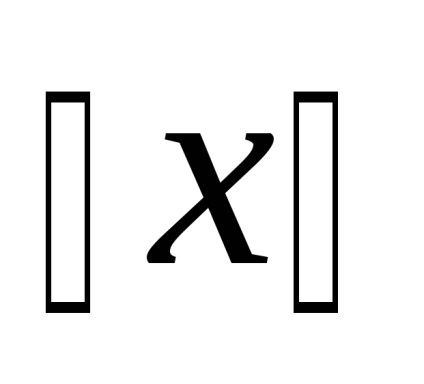
Tovább alsó becslés

Geller kínált:

Kapcsolódó cikkek

• Színezés hercegnő a Pea - gyerek színezés print ingyenes

• Tudd Intuíció, előadás, bevezetés lambda-kalkulus

• Tudd Intuíció, előadás, videó megfigyelő és videokártyák