Elmozdulás egyenes és ferde hasáb
Polyhedron nevezzük prizma, két oldala, amelyek egyenlők, poligonok fekvő párhuzamos síkokban, míg a másik oldalon - paralelogramma, amelynek közös oldalán ezen sokszögek. Ezek a paralelogramma nevezzük oldalfelületeinek a prizma, és a fennmaradó két sokszög nevezzük annak alapjait.
Prism egy konkrét esetben a henger. Egy doboz egy speciális esete a prizma.
A prizma a következő jellemzőkkel bír:
Bármilyen prizma párhuzamos metszeti síkban a bázis, ez prizma osztja két prizmát úgy, hogy az arány az oldalsó felületek és a térfogat aránya a prizmák egyenlő az arány a hossza az oldalsó élek. Bármely részén a prizma sík párhuzamos az oldalszél és osztja ezt a két prizma prizma úgy, hogy a térfogatának aránya ezeknek a prizmák egyenlő az arány a hossza az oldalsó élek. Bármely részén a prizma sík párhuzamos az oldalszél és osztja ezt a két prizma prizma úgy, hogy a térfogatának aránya ezeknek prizmák egyenlő aránya a bázis terület.
típusú prizmák
Prism. Az oldalsó szélei egyenes hasáb merőlegesek a alapsíkkal.
Ferde hasáb. Az oldalsó prizma élei vannak döntve a alapsíkon szögben eltérő $ 90 ^ \ circ $.
A helyes prizma. Az alapja az egyenes hasáb egy szabályos sokszög. Oldalsó arcok - egyforma négyzetekre.
Semiregular poliéder nevezzük egyenes hasáb oldallapjai, amelyek - négyzetek.
Térfogata egyenes hasáb
Levezetni képletek kiszámításához a hangerőt a rendszeres prizma prizma amelynek alapja a háromszög. Befejezés, hogy egy négyszögletes parallelepipedon (1. ábra).
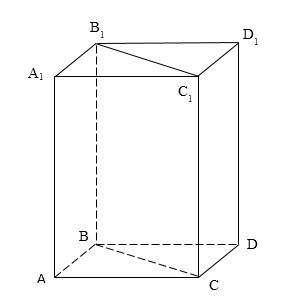
1. ábra: A tetraéder, befejezetlen fel a dobozt
Az előző fejezetben, tudjuk, hogy a kötet egy téglatest egyenlő:
mert kapott paralelepipedon tagjai az eredeti prizma és a prizma, egyenlő azt térfogatával, a térfogat az eredeti prizma lesz egyenlő
ahol $ a $, $ b $, $ c $ hosszúságú oldalakkal $ AB $, $ BC $, $ AC $, illetve, és hogy a termék megegyezik az eredeti terület a bázis a prizma, majd írt általános formájában egyenes hasáb képletű megállapítás térfogata:
ahol a $ S_ $ - négyzet alapú hasáb, $ H $ - magasság végre, hogy az alap a prizmát.
Ez a képlet helyes bármely egyenes hasáb egy sokszögű fenékkel.
Volume ferde prizma
A származtatott találni ferde háromszög prizma térfogata úgy ferde hasáb $ ABCDFE $. Döntetlen keresztül egy él síkja $ DC $ $ \ alpha $, hogy az alapra merőlegesen $ ABCD $ kezdeti prizma és a kivitelezést egy csonkított háromszögű hasáb (2. ábra).
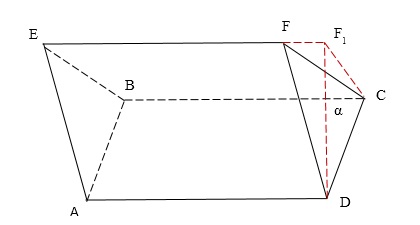
2. ábra: Ferde hasáb sík $ \ alpha $
Most át a szélén $ AB $ sík tölteni $ \ beta $, $ a párhuzamos sík \ alpha $ (3. ábra).
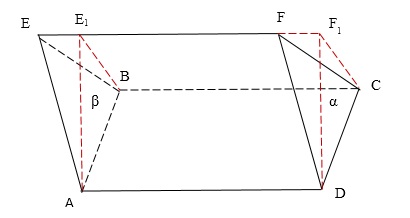
3. ábra: Ferde hasáb sík $ \ alpha $ és $ \ beta $
Ha alkalmazza a transzformációt a hajlam az arc újra, majd kapcsolja be a prizma, amelynek minden oldala nézzen merőleges az alapra. Ismét jobbra fordult prizmát.
Ha ki van téve, hogy a hasonló átalakításoknál (első kiegészítés első csonka prizma, majd vágjuk egy második csonka prizma), a befejezetlen és vágott prizmák párhuzamosan állnak fordítás a szegmens $ AB $. Ebből következik, hogy a számok azonos térfogatú.
Következésképpen, a kötet egy egyenes hasáb van kialakítva térfogata a kezdeti ferde.