Csökkentési képlet, tutomath
Csökkentési képlet nem kell tanítani őket, hogy megértsék. Értse az algoritmus kibocsátásuk. Ez nagyon egyszerű!
Vegyük az egység kör és helyeztük az összes intézkedést fokú (0 °, 90 °, 180 °, 270 °, 360 °) ellátva.
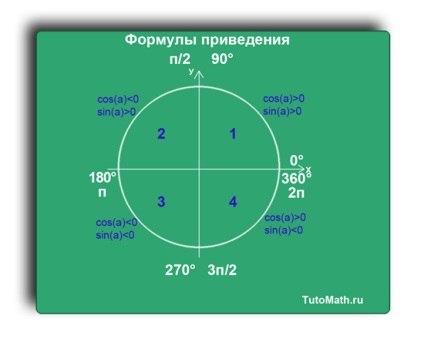
Elemezzük minden negyedében funkciók sin (a) és cos (a).
Ne feledje, hogy a függvény sin (a) nézi Y tengely és a funkció cos (a) az X tengely
Az első negyedévben látható, hogy a függvény sin (a)> 0. mert az Y tengely pozitív ebben a negyedévben.
És a funkciót cos (a)> 0. mert az X-tengely pozitív ebben a negyedévben.
Az első negyedévben leírható gradusnuju intézkedés (90-α), vagy (360 + α).
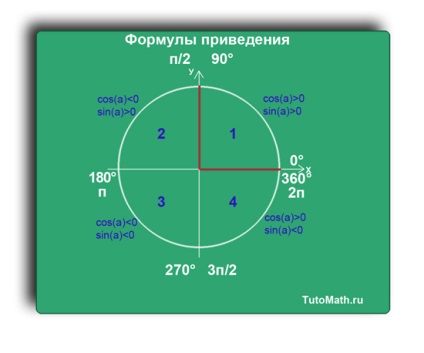
A második negyedévben, hogy a függvény sin (a)> 0. mert az Y tengely pozitív ebben a negyedévben.
Egy függvény cos (a) 0, mivel az X tengely pozitív ebben a kvadránsban.
A negyedik negyed-fok leírható az intézkedés révén a (270 + α) vagy (360-α).
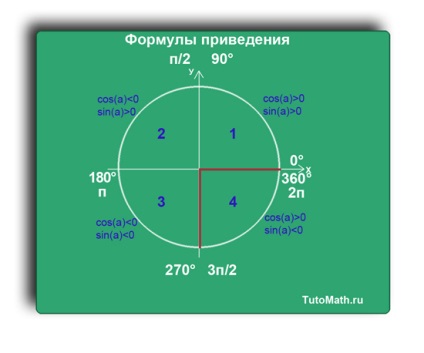
Most tartják magukat csökkentési képlet.
Ne feledje, egy egyszerű algoritmus:
1. negyed. (Mindig olvassa el a negyede van).
2. Bejelentkezés. (A negyedév néz pozitív vagy negatív függvénye cosinus, vagy szinusz).
3. Ha a zárójelben (90 ° vagy π / 2) és (270 ° -os vagy 3π / 2), a funkció változik.
És így kezdi szétszedni negyedévben az algoritmus.
Tudja meg, mi lesz egyenlő a kifejezés cos (90-α)
Mi jár az algoritmus:
1. A negyedévben az első.
2. Az első negyedévben a jele a koszinusz függvény pozitív.
3. A zárójelben (90 ° vagy π / 2), a függvény változik a koszinusz és szinusz.
Will cos (90-α) = sin (α)
Tudja meg, mi lesz egyenlő a kifejezés sin (90-α)
Mi jár az algoritmus:
1. A negyedévben az első.
2. Az első negyedévben a jele a szinusz függvény pozitív.
3. A zárójelben (90 ° vagy π / 2), a függvény változik a szinusz és koszinusz.
Ez lesz sin (90-α) = cos (α)
Megtudja, melyik egyenlő az expressziós cos (360 + α)
Mi jár az algoritmus:
1. A negyedévben az első.
2. Az első negyedévben a jele a koszinusz függvény pozitív.
3. A zárójelben van (90 ° vagy π / 2), és (270 ° -os vagy 3π / 2), a funkció nem változik.
Will cos (360 + α) = cos (α)
Megtudja, melyik egyenlő az expressziós sin (360 + α)
Mi jár az algoritmus:
1. A negyedévben az első.
2. Az első negyedévben a jele a szinusz függvény pozitív.
3. A zárójelben van (90 ° vagy π / 2), és (270 ° -os vagy 3π / 2), a funkció nem változik.
Will sin (360 + α) = sin (α)
Megtudja, melyik egyenlő az expressziós cos (90 + α)
Mi jár az algoritmus:
1. negyed másodperc.
2. A második negyedévben a jele a koszinusz függvény negatív.
3. A zárójelben (90 ° vagy π / 2), a függvény változik a koszinusz és szinusz.
Will cos (90 + α) = -sin (α)
Megtudja, melyik egyenlő az expressziós sin (90 + α)
Mi jár az algoritmus:
1. negyed másodperc.
2. A második negyedévben a jele a szinusz függvény pozitív.
3. A zárójelben (90 ° vagy π / 2), a függvény változik a szinusz és koszinusz.
Ez lesz sin (90 + α) = cos (α)
Megtudja, melyik egyenlő az expresszió COS (180-α)
Mi jár az algoritmus:
1. negyed másodperc.
2. A második negyedévben a jele a koszinusz függvény negatív.
3. A zárójelben van (90 ° vagy π / 2), és (270 ° -os vagy 3π / 2), a funkció nem változik.
Will cos (180-α) = cos (α)
Megtudja, melyik egyenlő az expressziós sin (180-α)
Mi jár az algoritmus:
1. negyed másodperc.
2. A második negyedévben a jele a szinusz függvény pozitív.
3. A zárójelben van (90 ° vagy π / 2), és (270 ° -os vagy 3π / 2), a funkció nem változik.
Will sin (180-α) = sin (α)
Vitatkoznak a harmadik és negyedik negyedévben módon teszik ki táblázat tartalmazza: