alkalmazások a származék

Home | Rólunk | visszacsatolás
Az egyik származéka alkalmazások - L'Hospital-szabály a számítás a határértékeket (abban az esetben, bizonytalanságok és):
2.31. Keresse meg a határértékeket L'Hospital-szabály:
funkciós vizsgálatban monotonitás,
Szélsőséges és dudor.
Aszimptota grafikonjának
Opredelenie.Kriticheskoy pont funkció y = f (x) egy pont, ahol a származék egyenlő nullával, vagy nem létezik.
Tétel. Ha az intervallum (a; b) a derivált pozitív / negatív, akkor az intervallum funkció növeli / csökkenti.
Tétel. Ha átmegy a kritikus pont a származtatott előjelet ettől a „+” „-” (a „-” és „+”), majd - a pont maximális (minimális) függvény
Definíció. Konvex függvény hívják fel (le) intervallumban (a, b), ha a pont ebben az intervallumban keletkezik alatt (lásd fent) érintők épített ezeken a pontokon. Az inflexiós pont a grafikon hívják a pontot, amely osztja azt részre különböző irányokba konvexitás.
Fedezze fel a funkciót a monotónia és a szélsőséges, konvexitás.
1. tanulmányozza a funkciót a monotonitást és szélsőséges.
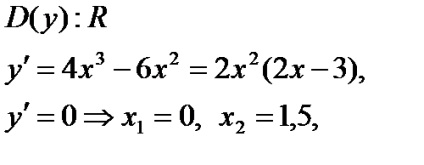
Készítsen rajzot (ábra. 2.1).
Kiszámítjuk az ordináta az inflexiós pontok grafikon:
A koordinátái inflexiós pontok: (0, 0), (1, -1).
2.32. Fedezze fel a funkciót a monotonitást és véglet:
2.33. Keresse meg a legkisebb és a legnagyobb znacheniyafunktsii:
1), az [2; 4];
2) intervallumban [-1; 1];
3) intervallumban [-4; 4];
4), az [-2; 1].
2.34. A termelési költségek C (.. y e) függ az összeg a kimenet x (u): Keresse meg a legmagasabb termelési költségek, ha x változik, az [2; 7]. Keresse az x értékét. amelyben a nyereség akkor maximális, ha a értékesítéséből származó bevételt a termelési egység egyenlő 15. e.
2.35. Azt akarod, hogy válasszon ki egy téglalap alakú területe 512 m2 és kerítés, és elosztjuk a kerítés három egyenlő részre párhuzamos egyik oldalon a platform. Mi legyen a terület méretét, hogy őr ment a legkevesebb anyagot?
2.36. Egy adott kerülete egy téglatest talált méretei úgy, hogy hiányzik a legnagyobb fény mennyiségét.
2.37. Keresse meg a maximális profit, ha a jövedelem az R & C költségek határozzák meg képletek: ahol x - az összeg az eladott áruk.
2.38. Függőség teljesítmény W teljesítmény a tőkeköltség a meghatározott feladat megtalálni a intervallum variációs K amelyen a tőkeemelés kiadások nem hatékony.
2.39. A célfüggvény értékesítéséből származó jövedelem egy egységnyi kibocsátás 200. Keresse meg az optimális értéket a gyártó termelési.
2.40. Függése a termelés volumene (pénzben) a tőkeköltség határozza meg a különböző függvény értékei a keresésben. amely a nagyobb beruházási költség hatékony.
2.42. Jövedelem termelés a forrás használata egységek olyan erőforrás érték Eladási ár - 10 den. u Milyen források összegét kell vásárolni a profit volt a legmagasabb?
2.43. A célfüggvény értékesítéséből származó jövedelem a termelési egység egyenlő 50. Keresse meg a maximális profit, hogy kaphat a gyártó.
2.44. Függés jövedelem monopólium a termékek száma definiáljuk a költség függvény ezen intervallum formájában találja meg a legjobb ár-érték a monopólium kimenet.
2.45. Az ár a termelési monopólium gyártó megfelelően van beállítva az arány azonosított. Milyen értéken történő felszabadulásának az árbevétel lesz a legnagyobb termelés?
2.46. költség függvény az alábbi űrlapot alatt. Abban a pillanatban, a kibocsátás szintje milyen feltételek mellett a p paraméter nyereséges cég a termelés csökkentésére, ha a jövedelem értékesítéséből származó egységnyi termelési egyenlő 50?
2.47. Keressen egy inflexiós pontot, és időközönként domborulata a függvény grafikonját:
2.48. Keresse meg a aszimptotája a grafikonon:
Megjegyzés. Vertikalnayaasimptotaimeet egyenlet x = a, ha legalább az egyik határok egyoldalú függvény x = a egyenlő ∞.
Naklonnayaasimptota amelynek egyenlete