A klasszikus meghatározás valószínűség
Vannak különböző megközelítések meghatározó a valószínűsége egy esemény.
Az egyik ilyen meghatározások az úgynevezett klasszikus definíciója valószínűsége. Úgy keletkezett a kezdeti fejlődési szakaszában az elmélet a valószínűség.
Ebben a meghatározásban valószínűségi események úgynevezett kapcsolatban meghatározott számú elemi esemény előnyben ezt Søby-Tia, az összes elemi esemény equipossible tapasztalat.
Annak a valószínűsége, egy esemény A jelöli a P (A). Ha ezek után kb m-átlag számú elemi eredmények kedvező esemény A és n - száma egyaránt lehetséges kimenetelét elemi élményt, amely egy teljes csoport események,
Létrehozása bizonyos tulajdonságait valószínűsége egy esemény.
Az ingatlan 1 valószínűségét egy esemény egy olyan nem negatív szám nulla és egy között: 0 <Р (А) <1.
Ez a tulajdonság közvetlenül következik a (19) képlet Mivel 0 Tulajdonság 2. A valószínűsége, hogy egy bizonyos esemény egyenlő egy: P (u) = 1. Ez abból a tényből következik, hogy egy bizonyos esemény bekövetkezik mindegyik vizsgálatban (m = n). Az ingatlan 3 valószínűség lehetetlen esemény nulla: P (V) = 0. Tény, hogy a esemény lehetetlen bármilyen vizsgálat nem-lépések (m = 0). Az ingatlan 4 (additív). Ha az A és B - összeegyeztethetetlen események, a valószínűsége az összegük összegével egyenlő a valószínűségek P (A + B) = P (A) + P (B). Példa. Legyen 80 rész, melyek közül 60 javítható, míg a 20 hibás. Annak a valószínűsége, hogy a tétel véletlenszerűen vett szemet zhetsya ép. Határozat. Nyilvánvaló, hogy azért, mert az alkatrészek száma, ami van. E. száma 80, 60 és többre nem kedvez 20. Ha X jelöli az esetben, ha a tétel javítható venni, amelyek a klasszikus ég meghatározása a valószínűsége, hogy ez az esemény az aránya a kedvező elemi eredmények a száma minden ravnovoz lehetséges. ezért További 170 gyártott alkatrészek a gépen, esztergált alkatrészek 8 nem felel meg a szabványnak. Mennyi a valószínűsége részeinek kiválasztására, amely nem felel meg a szabványnak. Controller, ellenőrzése a termékek minőségét 500, megállapították, hogy közülük 10 tartozik a második fokozat, és a többiek - az első. Naydi- kiválasztásának valószínűsége ezek a tételek az első osztályú, másodosztályú termék kiválasztása. Tíz kártyák írásbeli számjegy 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. A két közülük ki véletlenszerűen és halmozott a megjelenés sorrendjében, majd a kapott számot olvasni. Annak a valószínűsége, hogy a szám páratlan. Hat kártyák vannak írva betűkkel, d, h, o, u, x. Miután lökés-gombóc ki véletlenszerűen egy lapot a másik után, és megjeleníti azokat a sorrendben, ahogy történt. Annak a valószínűsége, hogy a kártya lesz írva a „levegő”. A dobozban van 6 piros és 9 fehér golyó. A box-távolítsa el az elakadt Cheny három golyót. Annak a valószínűsége, hogy közülük kettő piros lesz. A klasszikus meghatározás valószínűség azt jelenti, hogy minden elem-Tary eredmények egyformán valószínű. Körülbelül egyenlő lehetőségét eredményeken ops, amely általában következtetni szimmetria megfontolások (pl mint abban az esetben egy ideális kocka vagy érme). Ezek a problémák a gya-tic ritka. Sok esetben nehéz meghatározni az alapon számunkra azt feltételezni, hogy minden elemi eredmények egyformán valószínű. Ebben a tekintetben nem volt szükség, hogy vezessenek be egy újabb definíciója valószínűség néven ismertté vált a Staten-terrorizmus. Ez a meghatározás alapján egy ilyen koncepció, mint a relatív gyakorisága az esemény-CIÓ. Definíció. A relatív gyakorisága egy esemény vagy a frekvencia az arány a kísérletek száma, amelyben volt ez a Søby távú, hogy a szám minden kísérlet történt. Jelöljük a gyakorisága az esemény A-W (A), akkor értelemszerűen, ünnepély
6. Az gyakorisága az esemény. Statisztikai meghatározása a valószínűsége
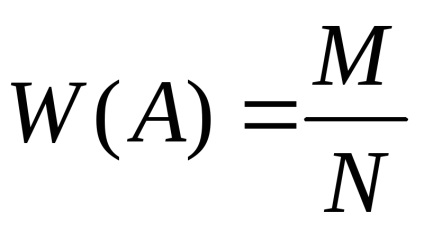
ahol M - a kísérletek száma, amelyben az esemény bekövetkezett, és N - száma minden kísérlet történt.
Az események előfordulási gyakorisága a következő tulajdonságokkal rendelkezik:
A frekvencia véletlenszerű események vannak száma nulla és egy között: 0 Frekvencia bizonyos esemény U jelentése egysége: W (U) = 1. Frekvencia lehetetlen esemény nulla V: W (V) = 0 A frekvencia összegének két diszjunkt események az A és B összegével egyenlő a frekvenciák ezen események: W (A + B) = W (A) + W (B) Annak a valószínűsége, P (A) az esemény A a statisztikai meghatározására úgynevezett frekvencia W (A) egy sor események álló fájdalom-SHOGO tesztek száma. Példa. A 600 véletlenszerűen kiválasztott 12 rész bizonyult elutasítása mi. Keresse meg a frekvenciát a hibás alkatrészek. Határozat. Mivel ebben a példában M = 12, és N = 600, akkor definíció van frekvenciaosztó 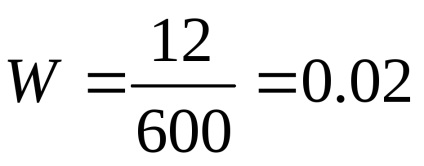
Megjegyzés. Emellett a fenti definíciók és a klasszikus statisztikai valószínűsége létezik, és az úgynevezett geometriai meghatározása valószínűsége. Az a tény, hogy mind a klasszikus mechanikai és statisztikai definíciók utalnak, hogy az elemek számát, Tary természetesen eredményeket. E hátrány kiküszöbölése, TSB-ditsya geometriai definíciója valószínűsége, miszerint a valószínűsége elfogadott terület egy bizonyos régióban SVOCs-csont, és elemi kimenetele - pont ezen a területen, feltéve, hogy minden elemi esemény a régió területén egyenlő 1.