A differenciálegyenlet a másodrendű, amelyek lehetővé teszik csökkentése a sorrendben

Home | Rólunk | visszacsatolás
Tekintsük a legegyszerűbb esetben másodrendű differenciálegyenletek, amelyek lehetővé teszik csökkentése érdekében.
1. A legegyszerűbb egyenlet ilyen típusú a következő egyenletet:
,
vagyis az egyenlet jobb oldalán csak attól függ, a független változó. Integrálása mindkét oldalán az egyenlet, megkapjuk. ahol - tetszőleges integráció.
Így a másodrendű differenciálegyenlet sok megoldásokat. Amint azt a fentiekben megjegyeztük, hogy megtalálja egy adott megoldást a szükségességét, hogy megfelelnek a kezdeti feltételek, azaz definiálni tetszőleges
Határozat. Mert. akkor. azaz. Aztán. Így.
Integrálása mindkét oldalán ezt a kifejezést, megkapjuk az általános megoldás a kezdeti egyenlet.
2. példa: talál egy adott oldatban. amely megfelel a kezdeti feltételek. .
Először keressük meg az általános megoldást. Ennek az egyenletnek kell következetesen integrálni. Figyelembe véve, hogy
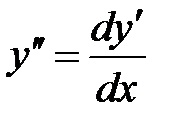
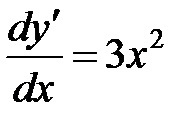
Szorozzuk mindkét oldalán az egyenlet. integrálni
.
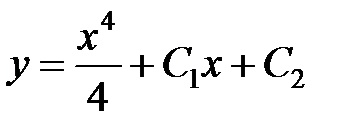
Most meg kell találni, és mivel a kezdeti feltételek. By hipotézist, majd
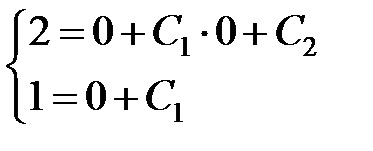
Ezért. . majd
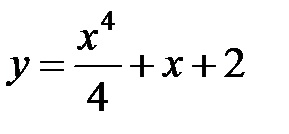
2. A differenciálegyenlet, hogy lehetővé teszi, csökkenti a sorrendben, típusát :.
A jobb oldalon az egyenlet nem tartalmazza a funkciója ismeretlen. Ebben az esetben az egyenlet megoldható helyett:
. .
Ennek eredményeként ez a helyettesítés egyenlet :. azaz, annak érdekében, csökken. Ezért elsőrendű differenciálegyenlet.
Határozat. Mivel az egyenlet nem tartalmazza a funkciója ismeretlen. akkor a megoldások használjuk helyettesítés: és. Aztán kapunk:
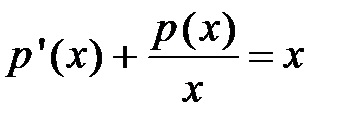
Egyenlővé a kifejezés, hogy áll az utolsó egyenletben zárójelbe nulla, ezt kapjuk:
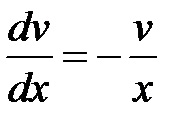
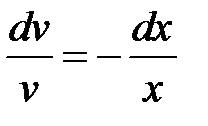
Integrálása mindkét oldalán az utolsó kapcsolatban megkapjuk. Ezért találni az ismeretlen függvény van differenciálegyenlet:
Így a funkció egyenlő :. Most azt látjuk, ezt a funkciót.
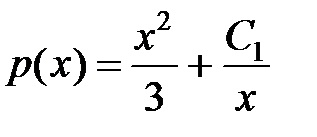
Mert. akkor van :.
Továbbá integrálásával mindkét oldalán az egyenlet, megkapjuk a végső megoldás az eredeti egyenletet:
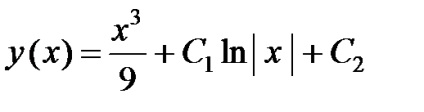
4. példa keresse meg az általános megoldást.
Határozat. Alkalmazza csere. hol. Ezt követően, az egyenlet válik :. Kapott egyenlet elkülöníthető változók
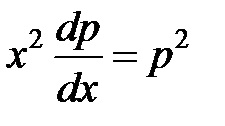
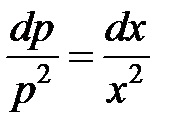
Vesszük a szerves mindkét fél
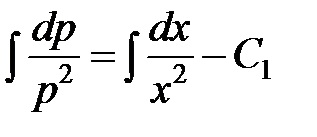
Tekintettel arra, hogy mi
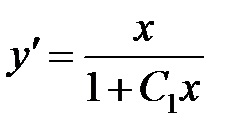
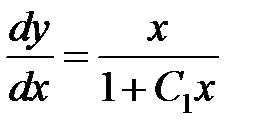
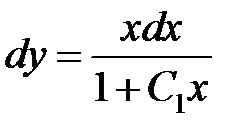
Integrálása mindkét oldalán az egyenlet
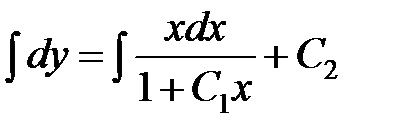
találni
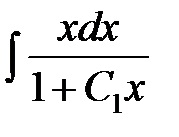
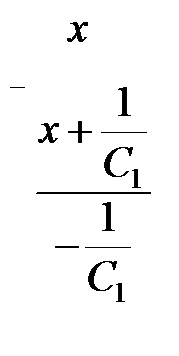
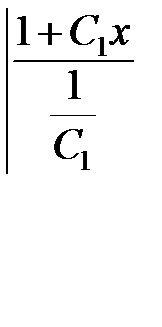
Integral formáját ölti
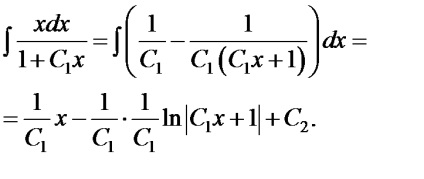
.
3. Az egyenlet, amely nem tartalmazza az érvelés. A jobb oldalon az egyenlet ebben az esetben nem tartalmazza a független változó és az oldatot lehet történő helyettesítésével kapott:
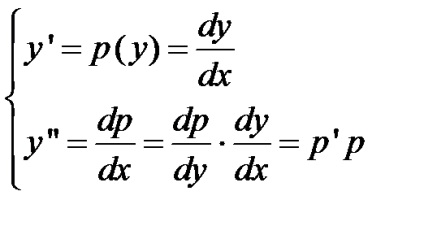
Behelyettesítve ismeretlen funkciójú, mind annak származéka, a kezdeti egyenletet, a differenciálegyenlet elsőrendű függvényében:
.
És kijelölő helyett pedig ezeket a kifejezéseket a kiinduló egyenlet, megkapjuk: - differenciálegyenlet elkülöníthető változókat. Elválasztó változók, megkapjuk:
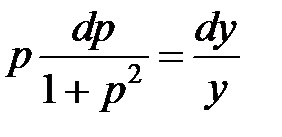
Integrálása mindkét oldalán az egyenlet, megkapjuk a teljes szerves a kezdeti differenciálegyenlet:
.