Orientált grafikonok ábrázolása - stadopedia
Az orientált grafikonok megjelenítéséhez különböző adatstruktúrákat használhat. Az adatszerkezet kiválasztása az operátoroktól függ, amelyeket a digraph csúcsaira és ívére alkalmaznak.
A G = (V, E) digfaph ábrázolásának egyik gyakran használt módszere a szomszédsági mátrix. Tegyük fel, hogy a V digraph csúcsai. akkor a gráf szomszédsági mátrix G - A jelentése egy méretű mátrix n n értékeket Boole-típusú, ahol A [i, j] = igaz, ha, és csak akkor, ha van egy ív vertex i vertex j. Gyakran a szomszédsági mátrix helyettesíti a valódi értéke 1 és értéke false - 0. Az időtényező hozzáférés szomszédsági mátrix méretétől függ a csúcsok halmaza és több ívek. Digráf képviselet formájában a szomszédsági mátrix kényelmesen használható a algoritmusokat, amelyek gyakran kell ellenőrizni a meglétét az ív.
A szomszédsági mátrix használatával lehetőség van a jelölt digráfok ábrázolására. Ebben az esetben az A [i, j] elem megegyezik az i j ív címkéjével. Ha az i csúcsból az j csúcsra nincs ív, akkor A [i, j] üres cellaként tekinthető. Az 1. ábrán. A 7.2. Ábrán látható a jelzett digraph és annak megfelelő szomszédsági mátrix.
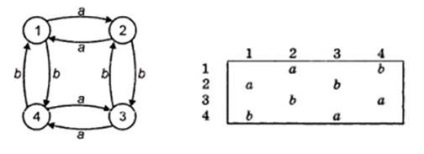
Ábra. 7.2 - A jelzett digraph és annak megfelelő szomszédsági mátrixa
A szomszédossági mátrixok fő hátránya, hogy a memória kapacitása akkor is egyenlő, ha az ívek lényegesen kisebbek. Ezért a mátrix elolvasása vagy a benne levő szükséges elem megtalálásához rendelési idő szükséges. ez nem teszi lehetővé az algoritmusok létrehozását az n időtartammal az n ívek sorrendű digráfokkal való együttműködéshez.
Ezért a szomszédsági mátrixok helyett a kontrasztlisták segítségével a digraph ábrázolása használható. Az i csúcsra vonatkozó szomszédsági lista az i csúcs melletti csúcsok listája. és bizonyos módon megrendelték. Így a G digraphot a HEAD tömb segítségével lehet ábrázolni. amelynek HEAD [i] eleme az i csúcs szomszédsági listájának mutatója. A kontrasztlisták használatával a kontrasztlistákkal való ábrázoláshoz olyan tárolókapacitás szükséges, amely arányos a csúcsok összegével és a tárolni kívánt ívek számával. Ha az ívek száma rendben van n. akkor a szükséges memória teljes mennyisége ugyanolyan sorrendben van. De a szomszédsági listák esetében egy adott ív keresési ideje lehet az n sorrendje, mivel Ugyanez a sorrend lehet az ívek számát egy bizonyos csúcson. Az 1. ábrán. A 7.3. Ábrán látható az 1. ábrán látható digraphot ábrázoló adatszerkezet. 7.1 a kapcsolódási pontok kapcsolódó listáin keresztül. Ha az ívek címkével vannak ellátva, akkor azok a kapcsolódó listák celláiban tárolhatók. A szomszédsági listákban lévő elemek beillesztéséhez és törléséhez rendelkeznie kell HEAD tömbvel. Tartalmaz egy mutatót a szomszédsági listák fejlécének sejtjeire, de nem maguk a szomszédos csúcsok.
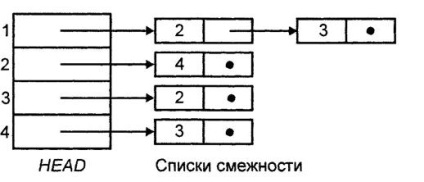
Ábra. 7.3- A digraph szomszédsági listájának szerkezete