Know-how, előadás, játékelmélet
Kivonat: Mielőtt elkezdené megismerni a gazdasági mechanizmusok elméletét, elengedhetetlen lesz egy kis idő az elmélethez, ami feltétlenül szükséges ahhoz, hogy megértsük mindazt, ami a mechanizmusok kialakításában történik. A beszéd ebben a bevezető előadásban a játékok elméletéről szól.
Alapfogalmak
Adjunk egy hivatalos meghatározást a játékokra, amelyeket fontolóra vennünk. By the way, a sakk, vagy akár megy nem esik e meghatározás alá. Ami logikus: foglalkozunk matematika, és nem hatékony algoritmusok; és egy matematikai szempontból (és a szempontból az elmélet algoritmusok bonyolultsága, aszimptotikus jellegű) sakk, vagy megy teljesen érdektelen: az utolsó táblán az utolsó tétel időtartama és teljes körű tájékoztatást a győztes (vagy win-win, ha nyertes nem) stratégia lehet „könnyen "a változatok egyszerű keresésével számítható.
Játékok, hogy figyelembe vesszük is, általában bevonják egy véges (vagy elmélet folyamatos, de a valóságban mindegy végén a sor lehetséges árak, amelyeket a játékos kijelentheti aukció), az a lehetséges stratégiák. Ugyanakkor az információ elvben nem teljes; erről és az egész elméletről. A stratégiai játék megértésénél minden játékos egyszerre fog működni, és mindegyik nyereménye attól függ, hogy milyen stratégiákat választanak mindenki más.
Definíció 1.1 A stratégiai játék hármas
ha a jelölést a következőképpen értelmezik:
- - a játékosok végső sorozata.
- - a játékosok rendelkezésére álló cselekvéskészlet, ahol - a játékos számára rendelkezésre álló akciók. A játékos cselekvésén keresztül jelezzük, és a következőket: - minden játékos cselekvési vektorát, kivéve: i 1 Általában a könyvben szereplő típusmegjelöléseket mindenütt megtaláljuk - szokni fogunk. A játékosok akcióinak összes vektorának halmazát fogjuk megnevezni - a vektorok készlete minden játékos számára kivéve. A vektort cselekvési profilnak nevezik. vagy kimenetele.
- - Sok fizetési funkció.
Sokkal inkább érdekelnek a cselekvések, hanem a stratégiák. A stratégia az, hogy az ügynök hogyan választja meg tevékenységét. A játékelmélet kezdetén ez ugyanaz, de a gazdasági mechanizmusok elméletében olyan stratégiákat veszünk figyelembe, amelyek olyan cselekvések vagy funkciók valószínűségi eloszlásait veszik figyelembe, amelyek figyelembe veszik a további információkat is.
Van még egy fontosabb megfigyelésünk: az előadás során azt feltételezzük, hogy a résztvevőknek preferenciái vannak a játék kimeneteleiről, és ezek a preferenciák funkcionalitással fejezhetők ki. Ez nem mindig van így, és a „Arrow-tétel és a Gibbard-Satterthwaite” fogunk beszélni érdekes hatásokat merülnek fel, amikor egy preferencia így lehetetlen kifejezni. De a játék alapvető elméletére vonatkozóan ezt a feltevést még meg kell tenni.
Ha a stratégiák halmaza véges, akkor a játék kimenetének halmaza egy -dimenziós mátrixsal fejezhető ki, amelynek cellájában az eredmények a koordináták. Két játékos esetén ez a design a leggyakoribb mátrixgá válik.
Az 1.1. Példa vége.
1.2. Példa. Második példaként tekintsük Blotto ezredes klasszikus játékát [70, 79]. Blotto ezredes köteles erõit (katonákat) terjeszteni a csatatér (ek) több részébe. Ellenfelének ugyanazt kell tennie (a katonái száma eltérhet). A győztes az, aki több csatatéren nyer.
Például, hagyja, hogy a harci területek a játékban három, és mind Blotto és az ellenfél három katona. Ezután a harc mindkét résztvevőjének stratégiája a következő elemekből áll:
Ennek eredményeképpen ez a játék kiderül, hogy ez az a mátrix. Itt Blotto stratégiái a bal oldalon vannak ábrázolva, az ellenség a tetején van; azt jelenti, hogy Blotto legyőzte - az ellenfél - egy rajzot.

1.2. Példa vége.
Megjegyezzük, hogy az 1.1. És az 1.2. Példában bemutatott játékokban egy résztvevő nyeresége szigorúan megegyezett a második veszteségével. Az ilyen játékokat zéró összegű játékoknak nevezik; hivatalosan szólva, ilyen játékokban a résztvevők tevékenységének bármely profiljához igaz.
A következőkben nemcsak a véges stratégiákkal rendelkező játékokkal fogunk érdeklődni, hanem folyamatosan hasonló készletekkel is. Vegyük a klasszikus példát - a Cournot verseny 3 Ez a példa az Antoine Augustin Cournot klasszikus közgazdasági elméletéhez [14] nyúlik vissza.
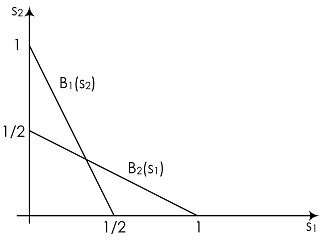
Ábra. 1.1. A Cournot versenye: az optimális válasz funkciója
1.3. Példa. Tekintsük egy termék piacát, amelyen pontosan két vállalat létezik :. Az egyes résztvevők stratégiája az általa termelt termék mennyisége :.
A játék eredményeként az egyes résztvevők nyeresége a teljes árbevétel mínusz a vételár:
hol van egy funkció. amelyen meghatározzák az árat, és - a vállalat egységenkénti árát. Ezt feltételezzük. Funkciót tekintjük
Próbáljuk megvizsgálni, hogy a cégek jobban tudják játszani a játékukat. Próbáljunk optimális stratégiát kialakítani a játékos számára, ha a játékos előállította az árut (a legjobb válasz funkciót). Ha, akkor semmit nem kell előállítani, mert az egyensúlyi ár továbbra is nulla lesz. Ha az optimális stratégia így fog kinézni:
Lásd az ábrát. Ábra. 1.1. amelyen ezeket a funkciókat ábrázoltuk. Intuitíven azt akarom mondani, hogy az egyensúly elérése a kereszteződésük pontján történik; de hivatalosan erről az alábbiakban fogunk beszélni.
1.3. Példa vége.