A kinematikus párok osztályozása
Idő Hosszúság Tömeg Angle lakás haladási sebessége pont lineáris sebessége sarokban gyorsulás lineáris frekvencia szöggyorsulások forgási tehetetlenségi nyomatéka az anyag sűrűsége Teljesítmény Nyomaték Nyomaték Működtetés kinetikus energia
Meter Kilogram Másodszor radián, fok mérő mérő másodpercenként Radian másodpercenként méter per szekundum a négyzeten radián per másodperc a négyzeten A rpm kilogramm per köbméter kilogramm négyzetméter Newton Newton-mérő-mérő Joel Watts
m kg rad, # 945; 0 m m / s rad / s, 1 / c m / s 2 rad / s 2. 1 / c 2 fordulat / kg kg / m 3 kg. m 2 N (kg m / s 2) Nm Nm J = Nm JW (J / s)
A MECHANIZMUSOK SZERKEZETE ÉS OSZTÁLYOZÁSA
A mechanizmusok szerkezete szilárd anyagokat tartalmaz. amelyek linkek. A kötőelemek nem lehetnek szilárdak (például egy öv). A hidrogén- és pneumatikus mechanizmusokban lévő folyadékok és gázok nem tekinthetők összekötőnek.
A mechanizmusok kinematikus sémáihoz kapcsolódó kapcsolatok feltételes ábrázolását a GOST szabályozza. Néhány kapcsolódás képét a 6. ábrán mutatjuk be. 1.1.
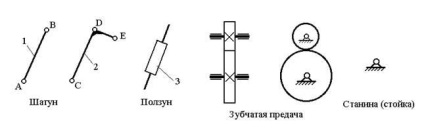
a mechanizmusok kinematikus rendszereiről
- input (vezető) - fémjelzi őket, hogy az elemi munka az alkalmazott erő a számukra pozitív (a munkaerő pozitívnak tekintik, ha az erőhatást iránya egybeesik a mozgás irányát annak az alkalmazás helyétől vagy hegyes szögben rá);
- kimenet (slave) - a rájuk alkalmazott erők elemi munkája negatív (az erő mûködése negatívnak tekintendõ, ha az erõ hatásának iránya ellentétes az alkalmazás pontjának mozgási irányával);
- fix (ágy, állvány).
A kinematikus sémákon a linkeket arab számok jelölik: 0, 1, 2, stb. (lásd az 1.1. ábrát).
A két érintkező kapcsolat mozgó kapcsolatát kinematikus párnak nevezzük. Lehetővé teszi az egyik kapcsolat relatív mozgását a másikhoz képest.
A kinematikus párok osztályozása
1. A következő kinematikus párokat a kapcsolatok összekapcsolásának elemei szerint osztják el:
- magasabbak (például fogaskerekes és bütyköstengelyes mechanizmusok) - a kapcsolatok összekapcsolása egymással egy vonalon vagy egy ponton történik:
- a legalacsonyabb - a kapcsolatok egymással való összekapcsolása a felszín felett történik. Az alacsonyabb összeköttetések pedig megosztva vannak:
2. Az egymásra helyezett kapcsolatok száma. A test, amely az űrben van (az X, Y, Z Descartes-koordinátarendszerben) 6 fok szabadsággal rendelkezik. Az X, Y és Z tengely mindegyikén mozoghat. Mindegyik tengely körül forog (1.2 ábra). Ha a test (kapcsolat) egy kinematikus párt alkot egy másik testtel (link), akkor elveszít egy vagy több ilyen 6 szabadsági fokot.
A test által elvesztett szabadságfokok számával (link) a kinematikus párokat 5 osztályra osztják. Például ha a kinematikus pártot alkotó testeket (linkeket) 5 fokos szabadságvesztéssel veszítjük el, akkor ez a pár az 5. osztály kinematikus párja. Ha 4 fokos szabadságot veszítesz - 4. fokozat, stb. A különböző osztályok kinematikus párjait a 3. ábrán mutatjuk be. 1.2.
Ábra. 1.2. Különféle osztályok kinematikus párjainak példái
A szerkezeti és szerkezeti jellemzők szerint a kinematikus párok forgó, transzlációs, gömb alakú, hengeres stb.
A kinematikus párok által összekapcsolt számos kapcsolat kinematikus láncot alkot.
A kinematikus láncok:
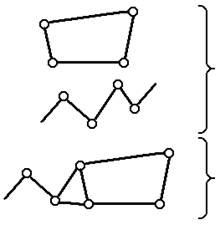
Egy mechanizmus kiépítése a kinematikus láncból. szüksége van:
- állítsunk be egy kapcsolatot álló helyzetben, azaz. keret létrehozására (rack);
- egy vagy több link a mozgás törvényének meghatározásához (vezető) oly módon, hogy az összes többi kapcsolat elvégezze a szükséges célszerű mozgásokat.
A mechanizmus szabadságfokainak száma a teljes kinematikai lánc szabadságfokának a rögzített linkhez (post) viszonyított száma.
Egy térbeli kinematikus lánchoz, általános formában, feltételesen jelezzük:
a mozgó kapcsolatok száma n,
a szabadságfokok száma ezeknek a kapcsolatoknak 6n,
az 5. osztály kinematikus párinak száma P5,
az ötödik osztály kinematikus párok által a kapcsolatokon feltüntetett kapcsolatok száma az SP5,
a 4. osztályú kinematikus párok száma P4,
a 4. osztály kinematikus párjai által a hivatkozásokon szereplő linkek száma 4P4, és így tovább.
A kinematikus lánc kapcsolata, amely kinematikus párokat alkot más kapcsolatokkal, elveszíti a szabadságfokok egy részét. A kinematikus láncnak az oszlophoz viszonyított szabadságának további számát a képlet alapján számolhatjuk ki
Ez a térbeli kinematikus lánc szerkezeti képlete, vagy a Malishev's formula, amelyet a P.I. Somov 1887-ben és az A.P. Malyshev 1923-ban.
A W mennyiséget a mechanizmus mobilitásának mértékéig (ha egy mechanizmus a kinematikus láncból alakul ki).
Egy sík kinematikus láncra, illetve egy sík mechanizmusra
Ezt a képletet PL-nek nevezzük. Chebyshev (1869). Ezt Malyshev képletéből lehet beszerezni, feltéve, hogy a gépen a testnek nincs hat, de három fokú szabadsága:
A W értéke azt mutatja, hogy mekkora legyen a vezető kapcsolatok mechanizmusa (ha W = 1 - egy, W = 2 - két vezető link stb.).