A statisztikák eszköztár funkcióinak listája
A Yarki-Ber-teszt a véletlen változó általános értéktartományának eloszlásának nem ellentmondására a normális törvényhez
H = jbtest (X)
H = jbtest (X, aa)
[H, P, JBSTAT, CV] = jbtest (X, aa)
A H = jbtest (X) függvényt arra tervezték, hogy elvégezzék a Yarki-Beer tesztet a slave értékek általános populációjának eloszlásának nem ellentmondásos normáljához az X.X mintából vektorként. A függvény egy skaláris H értéket ad vissza, amely a nullhipotézis tesztelésének eredménye, ami a kritikus szignifikancia szint 0,05. A null hipotézis az, hogy egy véletlen változó értékeinek általános népességének eloszlása nem ellentétes a szokásos törvényekkel. A Yarki-Ber-teszt alternatív hipotézise, hogy az általános lakosság eloszlása ellentétes a normális törvényekkel. Egy nullhipotézist kell elfogadni, ha h = 0 a. Ha H = 1, akkor a nullhipotézis elutasítható.
A Yarki-Ber-tesztet olyan esetekben alkalmazzák, ahol az általános népszámlálási aritmetikai átlag és variancia ismeretlen. Vizsgálat a null hipotézis alapján számítás ferdesége és csúcsossága az X minta esetén a nullhipotézis, a minta értéke az aszimmetria együttható kell kb nullával egyenlő, és a minta értékét kurtosis - három. Meg kell jegyezni, hogy a szovjet szakirodalomban feleslegben együttható határozza meg, ahol a képletben - együtthatója kurtosis, - a becsült pont a szórás, - a negyedik empirikus központi pont, - a minta átlag számtani - vektor minta értékek. Következésképpen a normális törvény kurtózis-együtthatója 0 lesz.
A Yarki-Ber-teszt során az aszimmetria és a kurtózis szelektív koefficienseinek eltéréseit a várt értékekhez viszonyítva határozzuk meg, feltéve, hogy a nullhipotézis egy adott minta méretére érvényes. Az aszimmetria és a kurtózis együtthatók mintaértékének eltéréseinek mértéke alapján khi-négyzet statisztikákat alkalmaznak. A Yarki-Ber tesztet nagy X mintamérethez használják. Kis mintaméret esetén a Lilliefors tesztet használják.
H = jbtest (X, alpha) Az alfa bemeneti paraméter lehetővé teszi a kritikus fontossági szint értékének beállítását a nullhipotézis teszteléséhez. Alapérték = 0,05. A nullhipotézis elfogadásának feltétele
hol van a jelentőség kritikus szintje? - a szelektív chi-tér statisztikáknak megfelelő szignifikancia szint. Az érték kiválasztása a kutató számára történik. A legtöbb gyakorlati esetben 0,05; 0,01.
[H, P, JBSTAT, CV] = jbtest (X, aa) A függvény kimeneti paraméterei: 1. a H nullhipotézis tesztjének eredménye egy adott kritikus fontossági szintre; 2. a k-kvadrikus statisztika szelektív értékének megfelelő P szignifikanciaszint; 3. A mintastatisztikák értéke chi-squareJBSTAT; 4. A chi-square CV statisztikák kritikus értéke. A nullhipotézis teszteléséhez a CV értéket használjuk. Ha a JBSTAT Példák arra, hogy a Yarki-Ber-teszt funkcióját a lakosság eloszlásának konzisztenciájára a normális törvények szerint alkalmazzuk A Yarki-Ber-teszt megfelel az általános lakosság normáljogának, a szelektív értékeknek megfelelően, a szokásos törvény szerint. A minta mérete 25 elem. A függvény a nullhipotézis tesztelésének eredményét adja vissza. A mintaértékek eloszlásának grafikus ábrázolását a függvény histfit segítségével végezzük.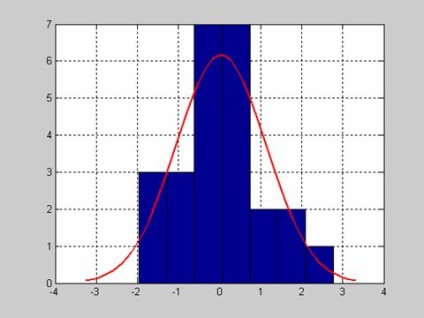
A Yarki-Ber-teszt megfelel az általános lakosság normáljogának, a szelektív értékeknek megfelelően, a szokásos törvény szerint. A minta mérete 30 elem. A függvény visszaküldi a nullhipotézis tesztelésének eredményét egy kritikus szignifikancia szintre, 0,01. A mintaértékek eloszlásának grafikus ábrázolása a qqplot függvény használatával történik.
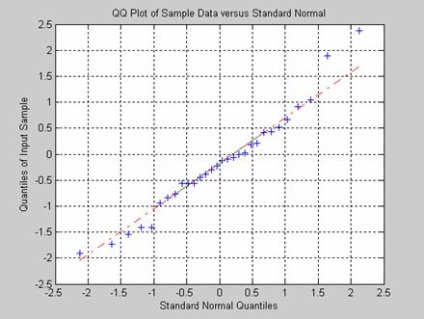
A Yarki-Ber-teszt megfelel az általános lakosság normáljogának, a szelektív értékeknek megfelelően, a szokásos törvény szerint. Az általános népesség eloszlása a normális és egységes törvények összetételét jelenti. A minta mérete 30 elem. A függvény visszaküldi a nullhipotézis tesztelésének eredményét egy kritikus szignifikancia szintre, 0,01. A mintaértékek eloszlásának grafikus ábrázolása a qqplot függvény használatával történik.
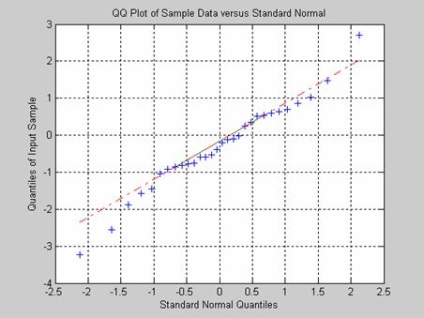
A Yarki-Ber-teszt megfelel az általános lakosság normáljogának, a szelektív értékeknek megfelelően, a szokásos törvény szerint. Az általános népesség eloszlása a normális és egységes törvények összetételét jelenti. A minta mérete 30 elem. A mintaértékek eloszlásának grafikus ábrázolása a qqplot függvény használatával történik. A függvény a nullhipotézis tesztelésének eredményét adja vissza egy kritikus szignifikancia szinten 0,01; a szignifikáns P szint, amely megfelel a chi-négyzet statisztikák szelektív értékének; a minta teszt khi-square értéke; a chi-négyzet statisztikák kritikus értéke.
A szignifikancia értékének függvénye a nullhipotézis tesztelésénél a minta méretére és az egységes jogszabály diszpergálására, mint egy x véletlen változó eloszlási törvényének összetételének. Az általános lakosság eloszlása a normális és egységes törvények összetétele. A normál komponens paraméterei állandóak és azonosak: a matematikai elvárás 0, a variancia 1. Az egységes komponens matematikai várakozása állandó, és feltételezik, hogy nulla.
>> sigma = 0: 0,1: 3 / 1,73;
>> n = 10;
>> i = 1: hossza (Sigma) x = normrnd (0,1, N, 1) + unifrnd (-1,73 * Sigma (i), 1,73 * Sigma (i), n, 1); [H, p1 (i), JBSTAT, CV] = jbtest (x); végén;
>> n = 20;
>> i = 1: hossz (sigma) x = normrnd (0,1, n, 1) + unifrnd (-1,73 * sigma (i), 1,73 * sigma (i), n, 1); [H, p2 (i), JBSTAT, CV] = jbtest (x); végén;
>> n = 50;
>> i = 1: hossza (Sigma) x = normrnd (0,1, N, 1) + unifrnd (-1,73 * Sigma (i), 1,73 * Sigma (i), n, 1); [H, p3 (i), JBSTAT, CV] = jbtest (x); végén;
>> plot (sigma, p1, 'vagy', sigma, p2, '+ b', sigma, p3, 'g')
>> grid on
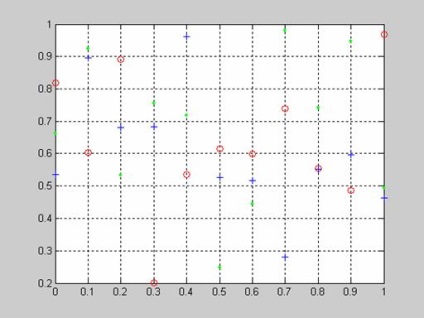
A szelektív chi-négyzet statisztikák eloszlásának típusa. Az általános lakosság eloszlása a normális és egységes törvények összetételének formája. A minta mérete 20 elem. A minták száma 25. A mintastatisztikák szokásos törvényének való megfelelés grafikus becslése a qqplot függvény használatával történik.
>> m_norm = 0;
>> sigma_norm = 1;
>> m_unif = 0;
>> sigma_unif = 3 / 1,73;
>> n = 20;
>> N = 25;
>> i = 1: N X = normrnd (m_norm, m_norm, n, 1) + unifrnd (m_unif-1,73 * sigma_unif, m_unif + 1,73 * sigma_unif, n, 1); [H, P, JBSTAT (i), CV] = jbtest (x);
>> qqplot (JBSTAT)
>> grid on