A határértékek módszere
Minden kérdés figyelembe vételével állandó és változó mennyiségek vannak.
Állandó mennyiségek Azok a mennyiségek, amelyek nem változtatják meg méretüket egy kérdés megvitatásakor, konstansoknak nevezik.
A mennyiségváltozók. Az értékeket megváltoztató mennyiségeket változóknak nevezik.
Ha egy kör van megadva, akkor ennek a körnek a sugara állandó érték, míg a körön fekvő bármelyik ponton áthaladó kör akkordjai változók.
Hasonlóképpen, a leírt rendszeres sokszög oldalainak számának növekedésével az apopémák állandó értékek maradnak, a peremek pedig változó mennyiségek.
A változók korlátok között változhatnak.
Hozzávetőleges érték. Amikor a változó során változás növelésével vagy csökkentésével közelít állandó érték, így a különbség közte és az állandó lehet kevesebb, mint az adott méretű, ez az úgynevezett közeledő mennyiséget.
Az állandó érték, amelyhez egy változó közeledik, annak határának nevezik.
A határ. A határ olyan állandó, hogy egy másik változó közeledik, növeli vagy csökkenti, de soha nem érte el, bár a különbség kisebb lehet, mint bármely adott érték.
A határértékek módszere. A tulajdonságok halmaza, hogy a közeledő mennyiségek és határaik, valamint ezeknek a tulajdonságoknak a alkalmazása különböző kérdések megoldására, a határmódnak nevezzük.
A korlát pontos definíciójától a korlát következő tulajdonságai követik:
A határ állandó érték.
A közelgő mennyiség mindig több, mint a határ.
A közeledő mennyiség és a határ közötti különbség kevesebb, mint bármely adott érték.
Az n oldalú, szabályos sokszög szögének összege a következő képlet segítségével fejezhető ki:
S = 2d (n-2) = 2.-4d
Minden szög értéke lesz
Ez az A érték egy változó. A szabályos sokszög oldalainak számának növekedésével változik.
Ebben a kifejezésben a 2d számnak mindhárom tulajdonsága van:
Először is, a 2d mennyiség állandó érték.
Másodszor, az A megközelítő értéke mindig kevesebb, mint 2d és
Végül a n növekvõ (4d) / n különbség kisebb lehet, mint egy adott érték.
A rendszeres sokszög növekvő számú oldalával minden egyes A szög értéke egyre növekvő mértékben közelít két egyenes vonalhoz, és két egyenes vonal az a határ, amelyre ez a mennyiség hajlamos.
Ha az X = K + α egyenletben az α mennyisége kisebb lehet, mint bármely adott mennyiség, és K állandó érték, akkor X közelítő mennyiség, és K a határ.
A határértéket a lim szó jelöli. (limitesen) vagy korábban. (határérték), a közeledés nagysága előtt.
Így írnak
K = lim X = lim (K + α)
Ebből az összefüggésből nyilvánvaló, hogy
Egy végtelen kis mennyiség olyan változó, amelynek nullpontja van.
A következő tételek fontosak a határmódszerben.
Tétel 129. Ha két közelítő mennyiség egyenlő, akkor a korlátok megegyeznek.
Ezt megadják. Legyen X és Y két megközelítő mennyiségű, A és B határértékeket, így
X = A + a, Y = B + β
Az α és β változók kisebbek lehetnek, mint bármely adott érték.
Bizonyítás. Attól a ténytől, hogy a két megközelítő mennyiség X és Y egyenlő, az egyenlőség X = Y vagy
Itt a következő három feltételezés fordulhat elő:
A> B, A
1. Ha van egy A> B egyenlőtlenség, akkor az A-B különbség egy bizonyos véges konstans k-val egyenlő.
Mivel a β és az α végtelenül csökkenhet, nem feltételezhetjük, hogy a β-α különbség megegyezik egy konstans véges értékkel k, ezért az A> B egyenlőtlenség lehetetlen.
2. Hasonlóképpen, az A egyenlőtlenség
ahol l állandó véges érték.
Az egyenlőségből (a) következik
Ez az egyenlőtlenség ugyanolyan lehetetlen, tehát az A feltevés Tehát csak az egyenlőség marad érvényben: A = B (BTD). A 130. tétel. A közeledő mennyiségek aránya megegyezik a határértékek arányával. Két közelítő mennyiséget adunk meg X = A + a és Y = B + β Kell bizonyítani, hogy X / Y = A / B. Bizonyítás. A két közelgő mennyiség aránya lesz Jelölje az aránynak véges értékét l-rel, majd A + α egy közelítõ mennyiség, amelynek A határértéke van; Bl + Bp egy hozzávetőleges mennyiség, amelynek határértéke Bl érték. Az előző tétel alapján az egyenlőség (1) egyenlőséget eredményez Következésképpen, l = A / B ahonnan (A + α) / (B + β) = A / B (BTD). A 131. tétel. A külső sokszögvonal nagyobb, mint a konvex görbe a sokszögvonalon belül.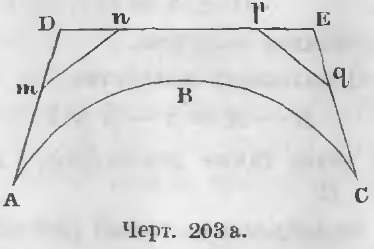
Bizonyítás. Ha az ABC görbe nem kevesebb, mint bármely külső sokszög (ábra. 203), akkor nem lenne léteznek, mint a külső sokszög, amely kevésbé lett volna, mint bármely más sokszögű külső és így kevésbé ABC görbéje.
Hagyja, hogy az ADEC legyen ilyen szakadt vonal.
Ebben az esetben, akkor mindig költeni szegmensek mn, PQ, így nem hatolnak át az ABC görbe, majd kialakult egy új vonallánc AmnpqC, ami kevesebb, mint ADEC, az
mn Ezekhez az egyenlőtlenségekhez hozzáadjuk az Am, np, qC mennyiségeket, amelyek: mn + pq + Am + np + qC Így a feltételezés, hogy létezik egy külső, sokszögű vonal, amely kisebb, mint egy görbe, nem tartja fenn. Ezért következik a következmény. A leírt sokszög körvonala nagyobb, mint egy kör. 132. tétel. Az ugyanazon név egy sokszögének a peremének különbsége, amelyet az oldalszámmal együtt írunk le és írunk be, kisebb, mint bármely adott érték. P és p jelöléssel a leírt és ívelt sokszögnek a n oldalakkal rendelkező vonalai (204. Ábra), tudjuk, hogy (P - p) / p = (OA - Oa) / Oa, (P - p) / p = Aa / Oa, P - p = (Aa / Oa) p (a) A poligon kerülete nagyobb, mint a belsejében bezárt poligon kerülete, ezért a perem p kisebb, mint a leírt tér kerületje. A leírt négyzet kerülete 8 · Oa (8 sugár), ezért p <8 · Oa. Ha a 8 · Oa beilleszti az egyenlőség (a) második részébe a p helyett, növeljük azt, P - p <8 · Oa · (Aa/Oa) или Megduplázásával az oldalak számát Aa szegmens hossza kisebb méretű lehet, mint bármely adott méretű, számának megkétszerezése az oldalán a szög AOB, és így AA szög csökken, és a ferde AO közeledő merőleges nO úgy, hogy a különbség a közvetett, és a merőleges lehet kisebb, mint bármilyen nagyságrendű. 133. tétel. Ahogy az oldalak száma nő, a leírt és beíródott sokszögek kerülete megközelíti a határt. Bizonyítás. Az egyenlőtlenségből Az oldalak számának megduplázásával csökken a leírt sokszög körvonala, és az ívelt kerület kerülete nő. Mivel az Aa határ értéke 0, a határérték (P - p) = 0. P = prev. p vagy lim P = lim p (PTC). 134. tétel: A kör a feliratokkal ellátott és leírt poligonok kerülete. Megduplázásával száma oldalán a kerülete sokszög leírni helyesen csökkenti és növeli a beírt kerülete. Ebben az esetben a leírt poligon kerülete nagyobb, és a beírt kör kisebb, mint egy kör. Mivel a különbség a kerülete a körülírt és feliratos poligon lehet kisebb, mint bármely adott érték, akkor minden bizonnyal fokozatos számának megkétszerezése oldalán a különbség a kerülete szabályos sokszögek leírt és egy kerülete, közötti és a kerülete, és a kerületük feliratos szabályos sokszögek lehet kisebb, mint bármely adott értéket ezért: A kör a beírt és leírt sokszögek kerületének határa. Tétel: 135. A körök arányosak a sugarakkal. Bizonyítás. Jelölje meg az O és O 'körök két körének hosszát, sugaraikat R és R' jeleken keresztül. Adjunk rendszeres poligonokat n oldalakkal mindkét körhöz. A Pn és Pn 'peremek jelölésével egyenlőségre van szükség akkor az előző egyenlet adja A fokozatos növekedése az oldalak számát különbségek a- és β között a köröket és a kerületük feliratos poligon lehet bármilyen kisebb ez az érték, tehát a különbség az O - α, O „- β értékek közeledtével és a mennyiségeket O és O” azok határait. A 130 Tétel alapján egyenlõség (O - α) / (O '- β) = O / O', Alapján O / R = O '/ R' vagy O / 2R = O '/ 2R' a következmény következik. az egyes köröknek az átmérőhöz viszonyított aránya állandó érték. A kerületi átmérő állandó arányát π betűnek nevezzük. A kerülete megegyezik a 2π-val megszorzott sugárral. Itt a hosszúságot ugyanabban az egységekben fejezzük ki, amelyekben a sugarat kifejezik. A π absztrakt száma nem egyezhetõ mennyiség. A 22/7-os megközelítő nagyságát Archimedes adja. A π valós értékét a 0.01-es értéken belül fejezi ki. Mecius, aki a 16. század végén élt, π közelítő értéke 355/113 = 3.141592 volt, pontossága 0,000001 volt. Ez az összefüggés könnyen megjegyezhető, ha a formában megjelenik Az ív hossza n fokkal. A kerület 360 ° -os. Az R sugarú kör hosszát a 2πR képlettel fejezzük ki. Az egyik fokozat hossza az érték (2πR) / 360. Jelölve, hogy s az ága n fokú ív hossza, akkor: Az (a) képlet három mennyiséget érint: n az ív, a hosszúság és a kör sugarának R számát. Lehetővé teszi a másik kettő közül egyet. Egy képlet, amely a kör kerületét fejezi ki, R = 1 formát vesz fel amiből látható, hogy a 2π egy kör sugara, amelyet egy sugár egyenlő. A π meghatározásához számítsd ki a rendszeres sokszögek körzetét, melyeket ugyanolyan oldalszámmal írunk le és írunk le. A kerület a két poligon kerületén belül van. Ez kisebb, mint a körülírt sokszögek és kerületek körvonala. A kerületek közötti különbség azt jelzi, hogy a kör definíciójában és így a π definíciójában milyen hiba van. Ennek a hibának a csökkentése érdekében a π definíció szerint egymás után kiszámolják a sokszögek kétszereseinek számát. A kerületek közötti különbség egyre kisebb lesz, következésképp növekszik a pontosság, amellyel meghatározható a π. A rendszeres sokszögek hosszának a hossza, amelyen n oldalak szerepelnek. Az An által leírt és az r által sugárzott rúd segítségével a képlet segítségével határozzuk meg az ívelt sokszög oldalhosszát kétszer annyi oldallal: hanem a leírt sokszög oldalának meghatározásához az oldal mentén az alábbi képletet: Pn és pn jelöli a leírt és beírt rendes poligon perimetrikus elemeit: A π közelítő értéke kielégíti az egyenlőtlenségeket: amelyben az a és az An egy 1-es sugárral rendelkező körre számítódik, ebből következően r = 1 a meghatározó képletekben. Az (1) és (2) képletek r = 1 esetén a következő formában vannak: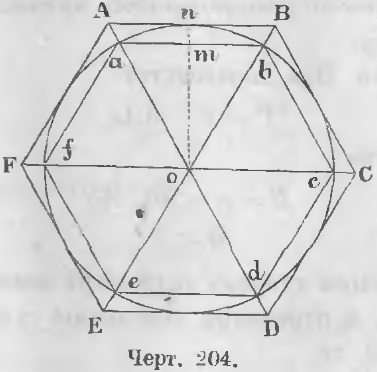
P - p <8AaA π definíciója
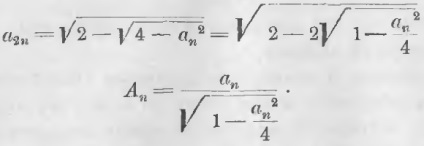
Feltételezve, hogy n = 6, a szabályos ívelt hatszög r = 1 oldalának a6 részére:

Ezeket az értékeket az oldalsó oldalak számával szorozzuk meg, a következő táblázatban a megfelelő számú oldalról rendszeresen írt és leírt sokszögek láthatók, számítva 6 tizedesjegy pontossággal

Ebből a táblázatból látható, hogy a szabályos sokszögek által írt és leírt peremek közötti különbség csökken.
A 96-gon esetében már kisebb, mint 0,01, és 3072 oldalas sokszög esetén kevesebb, mint 0,00001.
Archimédész telepedett le a 96-gon oldalának kiszámításánál, és megközelítette a π értékét 0,01-re. A Mecii a π értékhez π = 355/113 = 3.1415920 értéket adott 0,000001 pontossággal.