Statikus adatok mérése
Hartley-féle képlet nem tükrözi az események véletlenszerű jellegét, ezért általános esetben kapcsolat szükséges az információ mennyiségének és a releváns események (üzenetek) előfordulásának valószínűsége között.
Ezt a problémát 1946-ban az amerikai matematikus Claude Shannon orvosolta.
Statisztikai (valószínû) megközelítéssel az információ a megfelelõ üzenet elõfordulásának valószínûségének mértéke.
Ebből a szempontból, annál valószínűbb, hogy az esemény, annál kevésbé van információ az üzenetben.
Sokféle üzenet csökkenthető a kettős eseményekhez.
Általános esetben egy esemény tekinthető egy kísérlet kimenetelének eredményére. A helyzetek megoldásának minden lehetséges kimenetelének teljes csoportját az események együttesének nevezik.
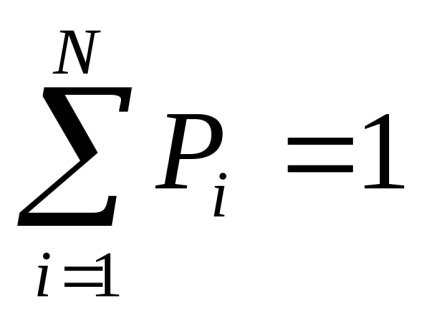
Hagyja, hogy az összes lehetséges kimenet összesen legyen N, melyből K nem ismétlődik.
Majd egy i-es esemény valószínűsége.
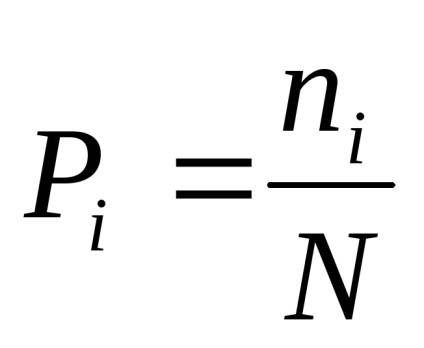
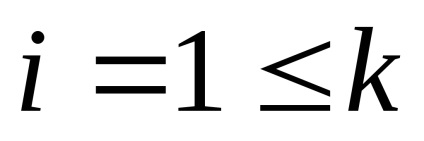
Az esemény végrehajtása bizonyos mennyiségű információt tartalmaz

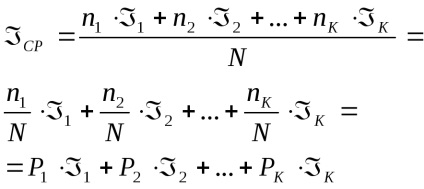
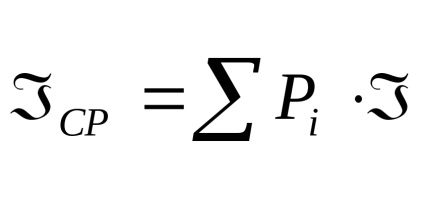
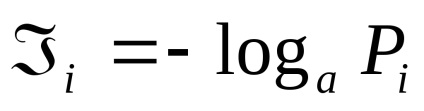
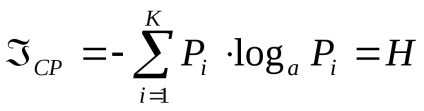
4 Az adatok statikus mértéke. Valószínűség és információ
Hartley-féle képlet nem tükrözi az események véletlenszerű jellegét, ezért általános esetben kapcsolat szükséges az információ mennyiségének és a releváns események (üzenetek) előfordulásának valószínűsége között.
Ezt a problémát 1946-ban az amerikai matematikus Claude Shannon orvosolta.
Statisztikai (valószínû) megközelítéssel az információ a megfelelõ üzenet elõfordulásának valószínûségének mértéke.
Ebből a szempontból, annál valószínűbb, hogy az esemény, annál kevésbé van információ az üzenetben.
Sokféle üzenet csökkenthető a kettős eseményekhez.
Általános esetben egy esemény egy kísérlet eredménye kimenetelének tekinthető. A helyzetek megoldásának minden lehetséges kimenetelének teljes csoportját az események együttesének nevezik.
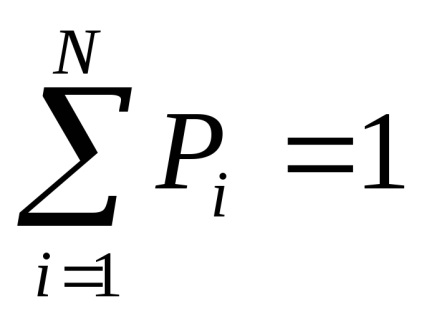
Hagyja, hogy az összes lehetséges kimenet összesen legyen N, melyből K nem ismétlődik.
Majd egy i-es esemény valószínűsége.
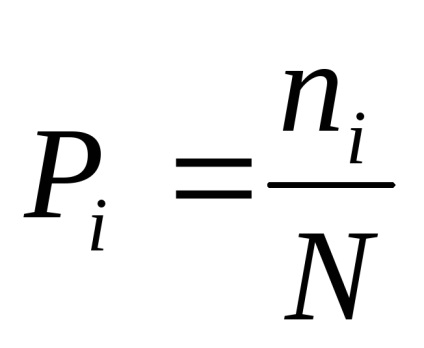
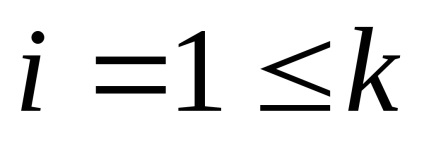
Az esemény végrehajtása bizonyos mennyiségű információt tartalmaz

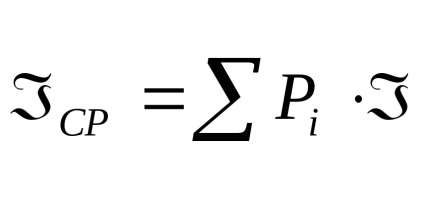
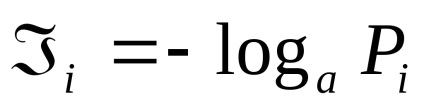
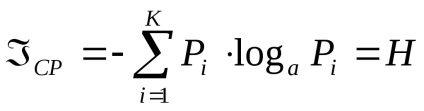
Entrópia tulajdonságai
1. Az entrópiát ugyanazon egységekben mérik, mint az információ mennyiségét.
A (2) képletben a "-" jel azt jelenti, hogy az entrópia mindig nem negatív, azaz
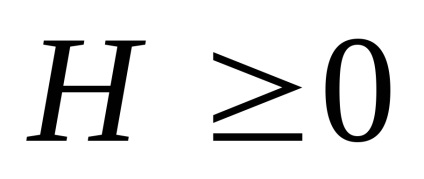
2. Az M entrópiája akkor érte el a maximális értéket, ha minden esemény egyformán valószínű.
3. H = 0, ha az i-es események egyikének valószínűsége 1.
Így az entrópia az üzenetforrás viselkedésében rejlő bizonytalanság mértéke, és jellemzi ennek a forrásnak az információ kiadását.
Ahogy a rendszer lehetséges állapotainak száma nő, az energia növekszik.
Általánosságban feltételezhetjük, hogy az információ mennyisége jellemzi az entrópia csökkenését a megismerés folyamatának következtében.
Ha a bizonytalanságot teljesen eltávolítják, akkor az energia mennyisége megegyezik a forrás által szolgáltatott információ mennyiségével.
A helyzet hiányos megoldása esetén az információ mennyiségét az entrópia kezdeti és végső értékei közötti különbség határozza meg:
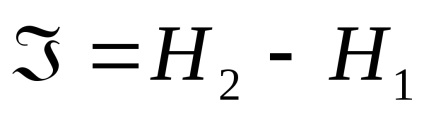
azaz Az információ mennyiségét a kezdeti és a végső entrópia értékek közötti különbség határozza meg.
A legnagyobb mennyiségű információ akkor jön létre, ha a bizonytalanság teljes mértékben megszűnik.
A valódi események, valamint a szimbólumok a valódi kapcsolatokban egymástól függetlenek és egyöntetűek, amelyek ténylegesen magukban hordozzák az egyes szimbólumokat, kisebbek lesznek a maximális elméletileg lehetséges értéknél.
Az információvesztést egy redundancia tényező jellemzi:
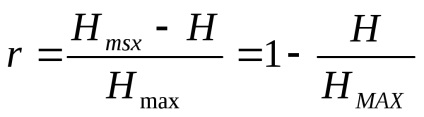
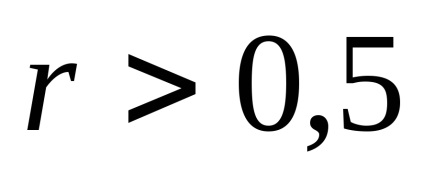
Az információs átviteli csatornák esetében a csatornák adatsebességének nevezett karaktert használják, ez egyenlő az egységnyi időegység alatt továbbítandó információ átlagos értékével.
Az üzenetegység forrása által az egységnyi időegységben keletkezett információ átlagos mennyiségét a forrás kapacitására hívják.
A csatorna maximális adatsebességét a csatorna sávszélességének nevezik.
A jelforrások teljesítményének és az átviteli csatornák kapacitásának összehangolásának problémája az információ kódolásának elméletének és gyakorlatának egyik legfontosabb feladata.