Konjugált funkciók
Az optimalizálási probléma megoldása
Azt mondhatjuk, hogy a konjugált funktorként egy adott probléma leghatékonyabb megoldását jelölik meg a standard módszer segítségével. Például egy elemi probléma az elmélet gyűrűk - hogyan kell bekapcsolni pseudoring (azaz gyűrű, amely multiplikatív egység) a gyűrűben. A leghatékonyabb módja ennek - felvenni a gyűrű egység, az összes elemet elvégzéséhez szükséges az axiómák gyűrű (. Például elemei a típusát, ahol r 1 r - gyűrűs elem), és nem utalnak arra, új kapcsolatok a gyűrűt, hogy nem szükséges, hogy végezze el a axiómák. Ez a konstrukció szabványos abban az értelemben, hogy minden pszeudo-gyűrű számára működik.
Azt mondani, hogy ez a módszer meghatározza a probléma "leghatékonyabb" és "standard" megoldását, ugyanaz, mint azt, hogy meghatározza a konjugált függvényeket.
A konjugált függvények több ekvivalens definíciója létezik. Ezek egyenértékűsége elemi, de nem triviális.
A meghatározás az univerzális nyíl segítségével [⇨] könnyen megfogalmazható, de a leginkább az "optimalizációs probléma" intuíciójához kapcsolódik.
Egy egység és egy megnevezés [⇨] meghatározása kényelmes olyan algoritmusok számára, amelyek gyakran előfordulnak az algebrában, mivel olyan képleteket kínál, amelyek közvetlenül ellenőrizhetők.
A meghatározás a Hom [⇨] készlet segítségével egyértelművé teszi a definíció szimmetriáját, és tisztázza annak okait, hogy a funktorok elnevezése "konjugált" legyen.
Univerzális nyíl
Mivel a terminológia azt jelenti, igaz, hogy az F - bal adjoint a G akkor és csak akkor, ha G - jobb adjoint F. azonban nem egyértelmű a meghatározása révén univerzális nyíl, de nyilvánvalóan definíciója miatt egységenként, és counit.
Egység és coedit
úgynevezett counit és a konjugáció egysége, azaz, hogy a kompozíciók
az F és G függvények 1F és 1G identitás-transzformációi.
Ilyen helyzetben F konjugátumot hagy G-ra és G helyes konjugátum F-hez. Néha ezt a kapcsolatot jelölik (ε. Η). F ⊣ G vagy egyszerűen F ⊣ G.
Az egyenletek formájában a fenti (ε, η) körülményeket counit és unit equations:
1 F = ε F ∘ F η 1 G = G ε ∘ η G 1 _ = \ varepsilon F \ CIRC F \ eta \\ 1_ = G \ varepsilon \ CIRC \ eta G \ end >>
A meghatározás a Hom függvényen keresztül
Ez határozza meg a családot:
minden X objektumra C-ben és Y-ban D-ben.
Itt F az úgynevezett bal konjugátum G és G a megfelelő konjugátum a F.
Ahhoz, hogy megértsük, mit értünk a Φ természetességével. meg kell magyarázni, hogy a homC (F -, -) és a homD (-, G -) függvények. Tény, hogy mindkettő kétfrekvenciás D op × C-tól Setig. Egy kifejezett formában a Φ természetesség azt jelenti, hogy minden morfizmus esetében f. X → X 'a C-ben és a morfizmusokat g. Y '→ Y-ban D-ben, a következő ábra átvált:
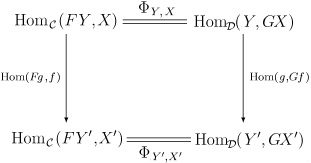
Szabad csoportok
Egy szabad csoport kialakítása kényelmes példa a definíciók lényegének tisztázására. Legyen F. Grp ← Állítsunk egy funktort, amely az Y és az G. elemek által generált szabad csoporthoz társítja Y-t → Set az elfelejtő funktort. amely X-hez kapcsolódik a hordozó készletéhez. Ezután F egy bal konjugátum G:
Terminál nyilak: minden X csoport esetében az FGX csoport az X csoport elemeinek által generált szabad csoport, mint készlet. Legyen ε X. FGX → X: FGX \ X> - csoport, homomorfizmus, amely lefordítja alkotó FGX a megfelelő elemeit X. Ezután (G X. ε X))> - terminális morfizmus F-ről X, mert minden homomorfizmus a szabad FZ csoport X végigsöpör ε X. FGX → X: FGX \ X> egyetlen funkciója a beállított Z a beállított X. Ez azt jelenti, hogy (F, G) - egy pár csatlakozómodulok funktorok.
A Hom készletek: az FY szabad csoporttól az X csoportig terjedő leképezések egyedileg felelnek meg az Y készlet leképezéseinek a GX halmazba. minden homomorfizmust egyedülállóan határoz meg az értékek a szabad csoport generátoraiban. Közvetlen számítással ellenőrizhetjük, hogy ez a megfeleltetés természetes átalakulás, ezért a páros (F, G) konjugátum.
További példák az algebrából
Példák a topológiáról
létezés
ahol az I. tételen futó algoritmusok olyanok, hogy bármilyen morfizmus:
lehet írni, mint:
egyesek számára én és néhány morfizmus:
Hasonló kijelentést mutatnak azok a függvénytulajdonosok, amelyek megfelelő adjoint tartalmaznak.
egyediség
Ellenkező irányban, ha F konjugált a G bal oldalán, és G természetesen izomorf, hogy G '. akkor F szintén G 'bal oldalán konjugált.
összetétel
A konjugációs kompozíciók természetes módon vehetők át. Ha
konjugált a funktortól balra