A binomiális terjesztési törvény
Az X diszkrét véletlen változó a binomiális törvény szerint kerül elosztásra, ha 0, 1, 2, ..., n értékeket vehet fel
a valószínűségeket, amelyek Bernoulli képletét találják:
Egy példa. Engedje meg a tudományos és technikai szövegből a három szóbeli formák önkényes kitermelését. Tekintettel arra, hogy a tudományos és technikai szövegben a főnév használata 0,4, az SV X esetében # 8209; "A választott főnevek száma", megtalálja az M (X) matematikai elvárásokat és a D (X) varianciát.
A megoldás. A CB X a binomiális törvény szerint kerül elosztásra, mivel a tesztek függetlenek, és a három kísérlet mindegyikének egy fõnevének valószínûsége állandó.
Itt n = 3, p = 0,4, q = 1-p = 0,6. Ezután M (X) = np = 3 0,4 = 1,2; D (X) = n p q = 3 0,4 0,6 = 0,72.
Az X diszkrét véletlen változót a Poisson-törvény szerint osztják el, ha 0, 1, 2, ..., n értéket vehet fel
valószínűségekkel, amelyeket a Poisson-képlet talál:
Egy példa. A 200 oldalas szöveg mindegyik oldalán található hiba valószínűsége 0,01. meghatározni:
a) a szövegben három hiba előfordulásának valószínűsége;
b) az M (X) matematikai elvárás és a D (X) CB X = "a szövegbeillesztés számának száma".
A megoldás. Mivel a hiba ritka esemény (p = 0,01), a Poisson képletet használjuk, hogy megtaláljuk a ritka események valószínűségét:
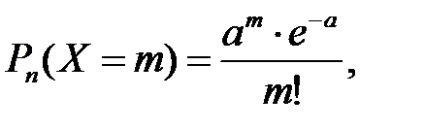
b) Egy X valószínűségi változó - „száma tipográfiai hibát a szöveg„Poisson-eloszlás, amelyre az M (X) = D (X) = A = 0,2.