A nemlinearitás fogalma
A nemlineáris és reológiai tulajdonságokon alapuló számítások perspektivikus módszerei
A talajbázisok kiszámításának problémáinak megoldására szolgáló nonlineáris megközelítés jelenlegi szakaszában két irány alapvetően kialakult - nemlineáris-elasztikus és elasztoplasztikus.
A nemlineáris elasztikus irány a nemlineáris függések és a deformációk (fizikai nemlinearitás) és deformációk és elmozdulások (geometriai nemlinearitás) függvénye. A legtöbb meglévő számítási módszerek geometriai jellegét nemlineáris figyelmen kívül hagyjuk, ami nem ismerhető meg minden csak ha figyelembe vesszük problémák nagy terhelés és magas értékei elmozdulás lehetséges előfordulásának határa egyensúlyi számítások vagy bázisok egymásra gyenge talajokon.
A nemlineáris rugalmassága egyenletek segítségével az egyensúly, és a geometriai és fizikai kapcsolatok, az első két egyenlet azonos használják rugalmassága és fizikai kapcsolatok gyakran használják, mint a generalizált Hooke-törvény, de változó attól függően, hogy a stressz szintjét állam: modulusa E törzs és a keresztirányú deformáció koefficiense v. Az értékek ezek a tulajdonságok alapján határozzuk meg a fenomenológiai (pilot) adatai szerint.
Nemlineáris problémák megoldásában a rugalmasság klasszikus elméletében alkalmazott integrációs módszerek nem alkalmazhatók. Ezért az egymást követő megközelítések módszerét kell alkalmaznunk, amely az integráció helyébe lép, a rugalmasság elméletében lineáris problémák sorrendjének megoldásával, az elasztikus megoldások módszerével.
Nemlineáris rugalmas megoldások megbízhatóbb eredményekre vezethet, mint a lineárisan rugalmas, de ne hagyjuk, hogy vegye figyelembe a számítás módja változások a külső terhelés (rakomány út), reológia deformáció és ferde a stressz és a törzs tenzorok. Ez kétségtelenül korlátozza a nemlineáris megoldások talajtömegre történő alkalmazását.
Elastoplastic megközelítés alapja külön leírást a rugalmas és képlékeny alakváltozások különböző fizikai függőséget. Szerint az ilyen ábrázolások, a használata differenciálegyenletek kapcsolatos a feszültség műanyag és a teljes törzs, valamint az eljárást lépés (egymást követő) feltöltése talajok összhangban annak érdekében, változás és külső terhelések alkalmazás lehetővé teszi, hogy figyelembe üzemmódba (pályagörbe) rakodási, valamint expresszióját eltolódás feszültség és az alakváltozás tenzorok és néhány egyéb sajátosságait a talaj, ami nem valósítható keretében a nemlineáris elmélet rugalmassága. Azonban a mérnöki problémák megoldásának ez a módja hátrányos. Különösen azt nem teszi lehetővé a nem-linearitás a rugalmas tartományban deformáció és áramlási folyamatokat a talajban előforduló.
A deformáció az idő a talaj tekinthető jelenleg az álláspontok az elmélet, az úgynevezett elmélet konszolidáció (tömörítés), beépített alapján használja a háromfázisú modell a talaj környezet, amely lehetővé teszi, hogy figyelembe vegyék a reológiai deformáció a talaj csontváz. Ez az elmélet azonban nem mentes bizonyos hátrányoktól, mivel főként a vízzel telített talajokat vonja el lineáris deformációban, ami nem mindig felel meg a talajművelés tényleges feltételeinek a szerkezetek alapjaiból.
Így most már a helyzet, ha a feszültség-alakváltozás a talaj állapotára nézve, itt egy olyan helyzetből különböző modellek (lineárisan rugalmas, nem-lineáris rugalmas vagy elastoplastic) és a Time csillapító csapadék becslések alapján a konszolidáció elmélete, amely más kezdeti feltételek esetén a különböző problémák megoldására használt kezdeti egyenletek megépítése. Így van értelme, hogy létrejöjjön a számítási modell, amely képviselné szintézise nemlineáris rugalmas és elasztikus műanyag elmélet és hagyjuk, hogy kövesse a folyamat a talaj deformálódását idővel.
A következő kezdeti feltevéseknek a modellen kell alapulniuk: a deformációk kicsi hipotézisének a végső értékek elmozdulása esetén érvényes értékei érvényesek; a külső terhelés időben változik bizonyos törvények szerint, változásának jellege statikus, vagyis a tehetetlenségi erő nem veszik figyelembe; A talaj csontvázának nemlineáris és reológiai tulajdonságai vannak, amelyeket fenomenológiai (kísérleti) adatok alapján határoztak meg.
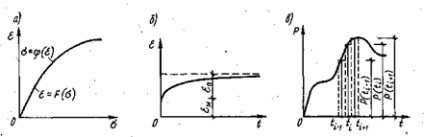
Ábra. 2.27. Függőségi grafikonok: a - stressz törzs; b - a csúszás idõ eltolódása; в - külső terhelés az időből
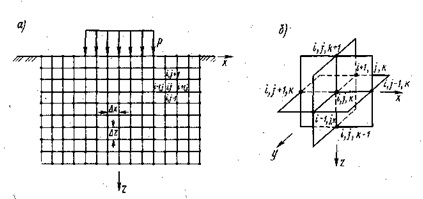
Ábra. 2.28. A bázis megoszlása a síkbeli (a) és térbeli (b) problémák véges különbségeinek módszerével
linearitását deformációja viszont egyenlet (2.50) függően Lame használt elmélet rugalmassága. Integrálása az egyenlet rendszert (2,50) a matematikai nehézségek merülnek fel határozatlan azonban a műszaki megoldások formájában numerikus módszert kell használni szerves becsléseket, amely lehetővé teszi, hogy linearizálásában probléma a fizikai régióban. A módszer lényege abban áll, rögzítési folyamatok és kúszási módban változó külső terhelés (ábra. 2,27 in) egy adott időszakban. Ez a megközelítés teszi a nemlineáris Integro-differenciálegyenlet (2,50), a lineáris differenciál az adott intervallumban betöltése. A megoldás ebben az esetben keresi segítségével a véges differencia módszer írva egy lapos vagy térfogatban (ábra. 2,28), és az egymást követő közelítését, amely lehetővé teszi, hogy cserélje több nemlineáris problémamegoldás rendszerek nemlineáris algebrai egyenletek másodrendű kezdve a rugalmas alakváltozás régióban. A kapott eredmény akkor tekinthető, ha a különbség a két utolsó iteráció kevesebb, mint egy előre meghatározott pontossággal számítás belül tartják időintervallumban.
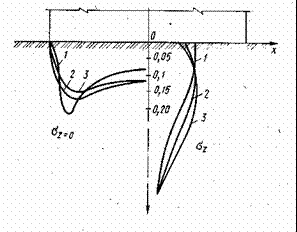
Ábra. 2.29. A merev bélyegző alapja a lineáris (1), nemlineáris rugalmas kúszó (2) bázissal és a kísérleti adatok eredményével (5)
Alkalmazása a számítási módszer, amely figyelembe veszi a nemlineáris és reológiai tulajdonságai alatt a deformáció talaj pincék, lehetővé teszi, hogy ne csak azok jobban megfeleljenek a valós tulajdonságait bázisok, hanem nyomon követni a viselkedését a feszültség-alakváltozás állapot alatt álló (változatlan) és nem stacionárius (változó) rakodási, így lehetővé téve, hogy megtalálják további tartalékok a szubsztrátum hordozó, ami megtakarítást jelent anyagi források az építési és működését az alapjait.
Cikkek a témában. Alapozási épületek és a gyártás biztonságát sooruzheniyTehnika konkrét rabotFundamenty ipari oborudovanieFundamenty speciális ipari sooruzheniyFundamenty zdaniyOsnovaniya fundamentyMetody és kiegészítését az alapítványokra rekonstrukció sooruzheniyFundamenty alatt szeizmikus vozdeystviyahMetody alapoz kiszámításának dinamikus hatásokat az ipari és háztartási oborudovaniyaUstroystvo bázisok olyan területeken, ahol állandóan fagyott