A hívásáramlás fő tulajdonságai
A véletlenszerű hívásáramlást az alábbi három tulajdonság jelenléte vagy hiánya alapján osztályozzák:
A stationaritás a bejövő hívások folyamatának egységességét jelenti, azaz a bejövő hívások folyamatának egységessége. A bizonyos számú hívás bizonyos ideig történő fogadásának valószínűsége függ a rés hosszától, és nem függ az idő tengelyének helyétől.
A helyhez kötött áramlást funkciók jellemzik - annak valószínűségét, hogy egy bizonyos ideig. pontosan meg fog tenni a hívásokat. Az ATC-hez ténylegesen érkezett hívásáramlás egyértelműen kifejezett, nem stacionárius jellegű, a hívásáram intenzitása lényegében a napi, a hét napja, sőt az év időtartamától függ. Egy napon belül azonban mindig egy óra időintervallumokat rendelhet, amelyek alatt a bejövő hívások áramlása közel áll a helyhez.
A rendszerváltozás a csoport bejövő hívások lehetetlensége. Két vagy több hívás valószínűsége bármilyen időintervallum esetén, ha az érték végtelen :. a
Utánkövetés - a hívásáramlás valószínűségi jellemzőinek függése a korábbi eseményektől. Vagyis a bejövő hívások valószínűsége a résen függ a hívás szolgáltatás számától, idejétől és időtartamától az időponthoz képest.
A kellően nagy forráscsoportból származó hívásáramlás hasonló tulajdonságaihoz hasonló a nem eseményáramláshoz (ha nem veszi figyelembe az ismételt hívásokat).
Éppen ellenkezőleg, a kis forrásokból származó áramlás észrevehető utóhatást vált ki. Tehát egy forráscsoport kapacitásával a hívások fogadásának valószínűsége jelentősen függ a szabad források számától és sokkal nagyobb lesz, ha. mint a. A szabad források száma viszont az előző eseményektől függ, ami meghatározza az áramlás következményeit.
A hívásforrások csoportjának kapacitásának növekedésével a foglalkoztatott források aránya fokozatosan csökken a teljes számhoz viszonyítva, és az áramlás utóhatása gyengül, és máris figyelmen kívül hagyható.
Utóhatás lehet:
1) korlátozott - amikor a különbség a hívások között. , ..., egymást kölcsönösen független véletlen változók sorozatát képezik;
2) egyszerű - azt jelenti, hogy az infinitezimális időintervallum felkínálásának valószínűségét a kapcsolórendszer állapota t időpontban határozza meg.
A hívásáramlások legfontosabb jellemzői
Az áramlás vezető funkciója az intervallumban szereplő hívások számának matematikai várakozása. Ez a funkció: nem negatív, nem csökkenő, gyakorlati problémák esetén a CT folyamatos, csak véges értékeket feltételezve.
A hurokban lévő hívásáramlás átlagos intenzitása az adott intervallumon belüli hívások számának matematikai várakozása.
A pillanatnyi intenzitást a következő adja meg:
Stacionárius áramlás esetén a vezetőfunkció egy időre megegyezik az áramlás intenzitásával, azaz:
Következésképpen a helyhez kötött áramlás intenzitása az időegységbe érkező hívások számának matematikai várakozása. Leggyakrabban az egy lecke átlagos időtartama egységnyi időre van kiválasztva.
Az áramlás paramétere a t időpontban a legalább egy hívás érkezési valószínűségének az időintervallumban lévő értékéhez viszonyított arányának a határa, ha:
A közönséges áramlások esetében van egyenlőség:
Álló áramlások esetén az áramlási paraméter nem függ az időtől :. Így a stationaritás és a ordinaritás tulajdonságait meghatározó véletlenszerű áramlás esetén írhatunk:
A legegyszerűbb hívásáramlás
A legegyszerűbb a hívások véletlenszerű átáramlása, amely egyidejűleg a stationaritás tulajdonságait, a szokásos és utóhatást nem jelenti. A legegyszerűbb áramlást teljes mértékben meghatározza a funkció, és engedelmeskedik Poisson törvényeinek:
Poisson a (2.6) képlet alapján, olyan táblázatokat hozunk létre, amelyek lehetővé teszik számunkra,
A (2.6) és (2.7) képletekből kiderül, hogy amikor az uuv (feltételes időegység) az u valószínüségeket csak u-tól függ. A növekvő Poisson-törvénysel folytonos normál eloszlási törvényre törekszünk (ha egy véletlen változó normális eloszlási törvényével egyeznek meg). A 2.2. Ábra mutatja az u értékének függőségében bekövetkező változásokat
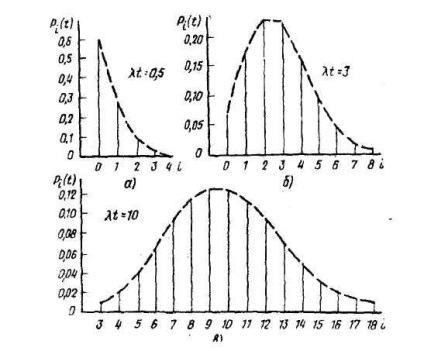
2.2. Ábra - A függvény értékétől való függőség.
A számok azt mutatják, hogy a maximális érték elérése:
1. Egy egész két ponton és;
2. Ha egy adott időpontban törtrészes
A legegyszerűbb áramlás tulajdonságai
1. Az "n" független elemi áramok és a paraméterek kombinálásával közös egyszerű áramlást hozunk létre a paraméterrel:
A pontos időkérések valószínûségét a Poisson-képlet és az áramlási paraméter a (2.8) képlet segítségével határozza meg.
2. A bejövő hívások számának minden lehetséges értékére vonatkozó valószínűség összege egy ideig egyenlő:
3. A hívások számának matematikai várakozása és varianciája egy adott időtartamra azonos és egyenlő:
Így a legegyszerűbb áramlásra
Primitív hívásáramlás
A véletlenszerű közönséges hívásáramlás egy olyan paraméter, amely egyenesen arányos a szabad forrásforrások számával egy adott időpontban, a primitívnek nevezve:
hol van a hívásforrások teljes száma?
- foglalkoztatott források száma;
- forrás paramétert szabad állapotban.
A primitív áramlást gyakran a második típusú Poisson áramlásnak nevezik (a legegyszerűbb az első típusú Poisson áramlás), vagy az Engsetovskii.
A primitív áramlás általánosabb koncepció a legegyszerűbb áramláshoz képest, és a legegyszerűbb.
A primitív hívásáramlás matematikai modellje a Bernoulli-eloszlás - a bejövő hívások valószínűsége a forrásból:
hol van a terhelés intenzitása egyetlen forrásból:
A bejövő hívás szervizelési ideje rögzíthető vagy véletlenszerű. A rögzített időt egy hk értékű sorrend adja. jellemezve a k-es hívás vagy a k-es hívócsoport szolgáltatási időtartamát. A karbantartási idő állandó lesz, ha a hk értéke h értéknek felel meg.
A hívási szolgáltatás véletlenszerű időtartamát a megfelelő véletlen változó eloszlásfüggvénye határozza meg. A legegyszerűbb és legelterjedtebb a terjesztési törvény:
ahol h a szolgálati idő matematikai várakozása.
Az exponenciális elosztási jog megválasztását az a tény magyarázza, hogy az utóhatás teljes hiányának tulajdonságai vannak.
A matematikai kifejezések egyszerűsítése érdekében a szolgáltatás időtartamának matematikai várakozása gyakran a szolgáltatás időtartamának mérési egysége, azaz a h = 1 USD
2.1. Melyik áramlást determinisztikusnak nevezik?
2.2 Hogyan határozható meg determinisztikus hívásáramlás?
2.3 Hogyan definiálható egy véletlenszerű hívásáramlás (definiált)?
2.4. Mit jelent az áramlás állóképességének fogalma?
2.5 Adja meg a "szokásos áramlás" fogalmát.
2.6. Mit jelent az "utóhatás utáni áramlás" fogalma?
2.7. Mi határozza meg a hívásáramlás intenzitását?
2.8.Mi meghatározza a hívásáramlás paraméterét?
2.9.A legegyszerűbb hívásáramlás meghatározása.
2.10 Milyen hívási folyamatot hívnak primitívnek?
2.11 Melyik hívásáramlás a legegyszerűbb?
2.12 Mi teszi lehetővé a képlet meghatározását?
2.13.Mivel lehet meghatározni az Erlang első eloszlásának képletét?
2.14 Mi lehet az első Erlang képlet meghatározása?