A grafikonelmélet története
A grafikonelmélet alapítója Leonard Euler. 1736-ban egyik leveleiben megfogalmazta és javaslatot tett a hét Koenigsberg-híd problémájára, amely később a gráfelmélet egyik klasszikus problémájává vált.
1. Az olyan gráfban, amelyen nincs páratlan erősségű csúcs, minden széle megkerülése (mindegyik éllel pontosan átmegy), a grafikon bármely csúcsa elindulásával.
2. Két és csak két páratlan ponttal rendelkező gráfban van egy kitérés, amelynek csúcspontja egy csúcs, a másik pedig vége.
3. Egy két fokú csúcsteljesítményű gráfban ilyen kitérés nem létezik.
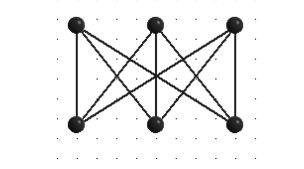
Van egy másikfajta feladat a grafikonokon való utazással kapcsolatban. Olyan problémákról beszélünk, amelyekben meg kell találni egy utat, amely minden csúcson áthalad, és legfeljebb egyszer egyenként. Minden egyes csúcson áthaladó ciklust hívnak Hamilton-vonalnak (William Rowan Hamilton, a múlt század híres ír matematikusa tiszteletére, aki először ilyen sorokat tanulmányozott). Sajnálatos módon még nem találtak általános kritériumot, amelyek segítségével lehetett eldönteni, hogy az adott gráf Hamilton, és ha igen, akkor megtalálja az összes Hamilton-vonalat.
A 19. század közepén készült. a négy színes probléma egy szórakoztató feladatnak is tűnik, de megpróbálta megoldani azt, ami olyan elméleti és alkalmazott jelentőségű grafikonok tanulmányozásához vezetett. A négyszínűség problémája a következőképpen fogalmazódik meg: "Bármelyik lapos térkép területét négy színnel lehet festeni úgy, hogy bármelyik két szomszédos terület különböző színekben legyen festve?". A hipotézis, hogy a válasz igenlő volt, a 19. század közepén született meg. 1890-ben gyengébb kijelentést bizonyítottak, nevezetesen, hogy minden lapos térkép öt színben van színezve. Bármely sík grafikon kettős lapos grafikonhoz való hozzárendelésével a probléma egyenértékű megfogalmazását kapjuk a grafikonok tekintetében: Igaz, hogy bármely sík grafikon kromatikus száma négy vagy annál kevesebb? A probléma megoldására irányuló számos kísérlet hatással volt a gráf elmélet számos irányának fejlesztésére. 1976-ban bejelentették a számítógép használatával kapcsolatos probléma pozitív megoldását.
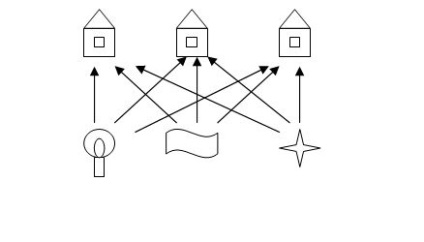
Egy másik régi topológiai feladat, amely egy nagyon hosszú időre nem reagált a döntésre és izgatta a puzzle-szerelmek elméjét, "a villamos energia, a gáz és a vízellátás problémája" néven ismert. 1917-ben Henry E. Djudeni adott neki ilyen megfogalmazást. Az ábrán ábrázolt három ház mindegyikében gáz, fény és víz szükséges.
Grafikus elmélet. 1
A grafikonelmélet eredete. 1
Euler szabálya. 1
1. Belov A Graph Theory, Moszkva, "Nauka", 1968.
3. OP Kuznetsov. Adelson-Velsky GM Diszkrét matematika egy mérnök számára. - M. Energoatomizdat. 1988.
6. Ore O. A grafikonok elmélete. - M. Science. 1980.