A grafikonelmélet eredetének története a stadopedia
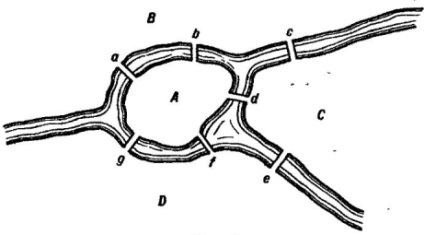
„Egyszer volt, felajánlotta a feladatot a sziget található a város Königsberg körülvéve egy folyó, mely ível hét hidat. A kérdés az, hogy valaki folyamatosan körülöttük csak egyszer kerülhet sor az egyes hídon. Aztán úgy értesült, hogy az egyik még mindig nem tudtam csinálni, de még senki nem bizonyította, hogy ez lehetetlen. a kérdés az, hogy bár banális, úgy tűnt nekem, de figyelemre méltó, hogy a döntését nem elegendő sem a geometria vagy algebra, vagy kombinatorikus art ... Sok gondolat után nem vagyok könnyű volt a szabály alapján igen meggyőző bizonyíték arra, hogy lehet használni az összes problémát az ilyen típusú azonnal megállapítani, hogy ott lehet elkövetett egy kis kitérőt néhány számot, és valahogy elrendezni hidak, vagy nem. Königsberg hidak úgy vannak elhelyezve, hogy azok lehet az az alábbi ábrán [1. ábra], amelyben egy jelöli szigeten, b, CiD -. a kontinens, elválasztva Bayou hét hidat jelölésére betűket a, b, c, d, e, f, g " .
Az általa felfedezett módszerrel kapcsolatban Euler leírta az ilyen problémák megoldását [vö. [5], p. 102-104]:
„Ez a döntés jellegénél fogva úgy tűnik, hogy kevés köze van a matematika, és én nem értem, hogy miért kellene inkább a matematika számíthat ez a döntés, nem pedig bármely más személy, mert ezt a döntést támasztja alá egyetlen paramétert, és nincs szükség bevonni megoldást találni, hogy minden törvényi rejlő matematika. Tehát, nem tudom, hogyan kiderül, hogy a kérdések nagyon kevés köze van a matematika, hanem hagyjuk a matematika, mint mások. "
Tehát lehetséges megkerülni a Koenigsberg-hidakat, és csak egyszer áthaladni ezeken a hidakon keresztül? A választ megtalálja, folytatjuk Euler levelét Marinoni-nak:
0 „A kérdés az, hogy miként kell meghatározni A szabály vezet a következő címre ezt a kérdést Először meg kell nézni, mert vannak olyan területek elválasztott víz, lehetséges, hogy kb mind a hét hidak, átmenő minden csak egyszer, vagy nem, .. - azok, amelyekben nincs más átmenet az egyik a másik, kivéve a hídon keresztül ebben a példában négy ilyen részek -. a, B, C, D. további meg kell megkülönböztetni, hogy a hidak száma ami ezeket a különálló területet, páros vagy páratlan Így a mi esetünkben öt híd van az A helyre és a többiekre ... Th - három híd, azaz a hidak száma, ami az egyes szakaszok, furcsa, és ez önmagában is elég ahhoz, hogy megoldja a problémát, amikor elhatározta, hogy alkalmazza a következő szabály: ha a hidak száma, ami minden egyes helyszínen, még az is , majd kitérőt kérdéses, lehetséges lenne, és ezzel egyidejűleg tudtuk kezdeni a túra bármely területen. Ha ezeket a számokat, két különös lenne, mivel csak egy lehet páratlan sem, még akkor egy átmenetet lehetett tenni, ahogy az előírta, de csak a bypass megkezdésének kell lennie a két helyszín egyikéből kell venni, amelyhez páratlan számú hidat vezet. Ha végül, már több, mint két terület, amely páratlan számú híd, akkor egy ilyen lépés nem lehetséges ... ha lehetséges volt, hogy itt más, súlyosabb problémát, ez a módszer lehet a még nagyobb haszon, és azt nem szabad figyelmen kívül hagyni " .
A matematikus azt írta, hogy az átmenet akkor lehetséges, ha a folyóág ágában nem több mint két régió van, amelybe páratlan számú hidat vezetnek. Annak érdekében, hogy könnyebben el tudjuk képzelni ezt, töröljük a rajzban már leírt hidakat. Könnyen belátható, hogy ha elkezdünk mozogni összhangban Euler szabályokat, át egy hídon, és kitörölni, akkor ez a szám jelenik meg station, ahol ismét nincs több mint két terület, amely páratlan számú hidak, valamint a területek jelenléte páratlan számú hidat találunk az egyikben. Folytatva így tovább, egyszer átmegyünk minden hidat.
A történelem a Koenigsberg városa hidakkal egy modern kiterjesztéssel rendelkezik. Nyissuk meg például a matematika iskolai tankönyvét, amelyet N.Ya szerkesztett. Vilenkina a hatodik osztályban. A 98. oldalon a tudatosság és a leleményesség fejlesztése alatt találunk egy olyan feladatot, amely közvetlenül kapcsolódik ahhoz, amelyet Euler egyszer megoldott.
Task number 569. A tóban hét sziget található, amelyek egymáshoz kapcsolódnak, amint az az 1.2. Ábrán látható. Melyik szigeten kell az utasok átadni a hajót, hogy áthaladhassanak az egyes hídon és csak egyszer? Miért nem vihetsz az A-szigetre?
A megoldás. Mivel ez a probléma hasonló a Koenigsberg-hidak problémájához, Euler uralmát is megoldjuk megoldásakor. Ennek eredményeképpen a következő választ kapjuk: a hajónak az E vagy az F szigetre kell szállítania az utasokat, hogy egyszer áthaladjanak az egyes hídon. Ugyanezen Euler-szabály követte a szükséges kitérítés lehetetlenségét, ha az A. szigetről indul.
Összefoglalásként megjegyezzük, hogy a Koenigsberg-hidak és hasonló problémák problémája, valamint a vizsgálati módszerek együttese a matematika nagyon fontos ágát képezi, gyakorlatilag a grafikonelméletnek nevezik. A grafikonok első munkája L. Eulernek és 1736-ban jelent meg. Később a grafikonokon dolgoztak Koenig (1774-1833), Hamilton (1805-1865), a modern matematikusok - K. Berge, O. Ore, A. Zykov.