Előadás 5
Ebben a részben a kettős és görbületi integrálokra vonatkozó képletet tekintjük.
. az integrált zárt kontúrra integráltnak nevezzük.
Engedje meg, hogy egy egyszerű zárt kontúr pozitív irányát hívja fel, amelynél a megfigyelő bal oldalán fekvő területnek a megfigyelőhöz legközelebb eső körvonal által határolt része található.
Tegyük fel, hogy u. azaz folyamatosan (D) és Γ egy zárt, részlegesen sima kontúr, akkor a következő képlet tartja:
,amelyet zöld formának neveznek.
A képlet kiszámításához az integrált értéket a zárt görbe fölé kell csökkenteni a görbe zárójelének integrálására.
A kimenetet több pontra osztottuk:
1) A D tartomány egy görbe vonalú trapéz:
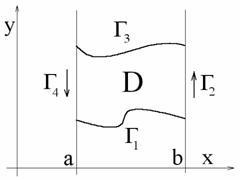
Most a kontúr felett az integrált formát írjuk. és a kettős integráció így fog kinézni:
- az egyenlőség első része bebizonyosodik.
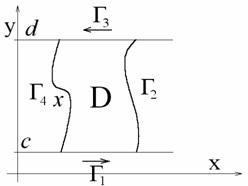
Most a görbe egyes szakaszainak integrálját írjuk, és a Γ2 és Γ4 integrálok egyenlőek a nullával:
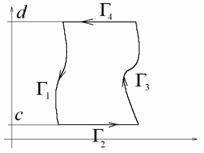
A dupla integrát a formában írjuk
. következésképpen ezt bebizonyítottuk. de korábban ezt is bizonyítottuk. ezért képviseltetheti magát.
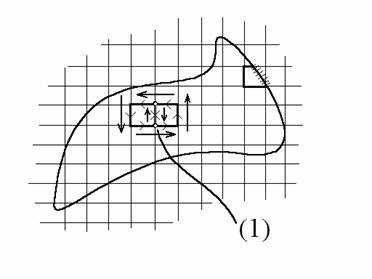
A két elem (1) határa mentén lévő integrál nulla, mivel kétszer ellentétes irányban számolódik ki, ezért az összes görbe-vonalú integrál összege megegyezik a D határvonala mentén lévő integrál összegével.
Most a Zöld képlet összetevőinek tekintjük.
A görbületi integrál függetlenségének feltételei
az integráció útjától egyszerűen összekapcsolva
területet a síkon
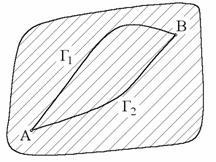
A következő négy feltétel az egyenértékűségi feltételek:
1) (az Γ1 és a Γ2 görbék azonos eredettel rendelkeznek - A pont és ugyanaz a B végpont)
2) az Γ bármelyik részlegesen sima zárt görbére vonatkozik.