Trigonometrikus funkciók
A trigonometrikus funkciók a szög funkciói. Különösen hasznos az időszakos események tanulmányozásában és modellezésében. Meghatározhatók a háromszög két oldalának aránya. Beleértve a szöget, vagy a pont koordinátáinak arányát egy körben, vagy általánosabban végtelen sorokként. vagy egy differenciálegyenlet megoldásaként.
Itt hat alapvető trigonometrikus függvény. Az utolsó négyet az első kettő határozza meg. Más szavakkal, ezek definíciók, nem független entitások.
1. Fogalommeghatározás
1.1. Geometriai meghatározás
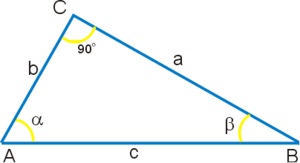
A szögek meghatározása egy derékszögű háromszög segítségével.
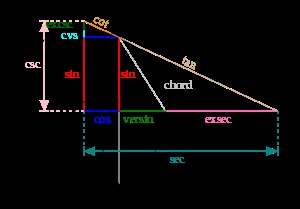
A trigonometrikus függvények meghatározása az egységlemezen.
A trigonometrikus függvények a jobb szögű háromszög figyelembevételével határozhatók meg.
A szög koszinusa a szomszédos láb hossza és a hypotenuse hosszának aránya.
A szög szöge az ellentétes láb hossza és a hypotenuse hosszának aránya:
A szög érintője az ellentétes láb hossza és a szomszédos láb hosszának aránya:
A cotangent szög a szomszédos láb hossza és a másik láb hossza aránya:
Hasonlóképpen, trigonometrikus függvényeket is definiálhatunk egy körön belül.
1.2. Kapcsolat a differenciálegyenletével
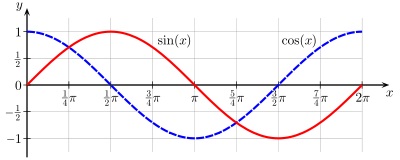
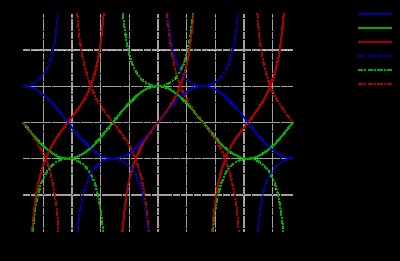
A függvények egy periódusa sin (x) és cos (x)
Az u függvények a harmonikus oszcillációk differenciálegyenletének megoldásai
és ezek periodikus függvények a periódussal
és van egy idő
Ratio alábbi kifejezésére használt értékek trigonometrikus függvények tetszőleges valós érv keresztül érv funkció értékeit intervallum
2. A fő kapcsolatok
A következő összefüggés Pitagorasz tételéből következik.
3. Tétel-tételek és képletek többszöggel
3.1. A szögek függvényeinek képletei
Az alapviszonyból
3.2. A kétszögek funkcióinak képletei
3.3. A háromszögek funkcióinak képletei
3.4. A félszögek funkcióinak képletei
3.5. A szögfunkciók összegének képletei
3.6. Általános képletek többszöggel
Ha n pozitív egész szám, akkor
4. A funkciófokok általános képletei
Ha n egy furcsa egész szám, akkor
Ha n egy egész szám, akkor
5. Taylor menetrendek
A Taylor sorozata a trigonometrikus függvények között létezik ilyen dekompozíció:
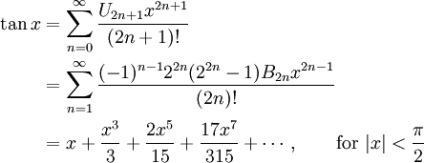
A Bostonfedon U n n-edik konverziója, B n Bernoulli számok. és E n az Euler szám.
5.1. Kapcsolat az exponenssel és komplex számokkal
A fenti osztályozás a Taylor-sor is bizonyítható, hogy a funkciók bűnnek és cos valós és képzetes része a művelői tisztán képzetes szám:
Ezt a kapcsolatot Euler-képletnek nevezik.
A z komplex változó trigonometrikus függvényeit definiálhatjuk:
ahol i 2 = -1, és u - ennek megfelelően hiperbolikus szinusz és koszinusz. A jelenlegi x, kapcsolatok