Határozza meg a raktár helyét, a raktár helyének meghatározására szolgáló módszereket, a meghatározást
A raktár helyének meghatározására szolgáló módszerek
Helyének meghatározásakor a raktár - az egyik alapvető megoldás a logisztika, amely tartozik a természet tervezési problémák és megoldani a tervezés logisztikai rendszerek. Ha összehasonlítjuk a meghatározása a raktár helye a fajta vezetői döntések, azt mondhatjuk, hogy ez a probléma a stratégiai döntések, alkotó eleme a beszerzés, mint a konfiguráció a logisztikai rendszer. Jellemzően a raktár helyének meghatározását az elosztó raktárakhoz viszonyítva kell figyelembe venni.
Annak érdekében, hogy meghatározzuk az elosztó raktár helyét a kiszolgált területen, szükséges tudni:
• a feldolgozóipari vállalatok (beszállítók) és a fogyasztók (vevők) elhelyezkedése, melyeket rendszerint a xp y koordináták adnak;
• Termékek (beszállítók) által a fogyasztóknak nyújtott termékek köre ((2,);
• a szállítási útvonalak, amelyek a meglévő közlekedési hálózat jellemzőitől függenek;
• szállítási költségek (vagy szállítási díjak) (7)).
A raktár helyének meghatározására különböző módszerek léteznek, amelyek különböznek az optimalizációs kritériumok és a beszállítók, a fogyasztók és a raktár közötti távolságok figyelembe vételével. Tekintsen kétféleképpen a távolságok figyelembe vételére. Az első módszer az, hogy kiszámolják a legrövidebb távolságot azok között a pontok között, ahol a beszállítók, az ügyfelek és a raktár található. A legrövidebb távolságot a képlet határozza meg
ahol x. y, - a szállító, a fogyasztó koordinátái; xc, ys a raktár koordinátái.
A második módszer a különböző távolságokra - az úgynevezett Manhattan távolság, amely a számla a távolságok szállítók és vevők közötti téglalap alakú rács, amely a legjobban megfelel a téglalap alakú elrendezése utcákon. A "Manhattan távolság" az alábbi képlettel számítható:
Azon kritériumok, amelyek alapján a raktár helyét meghatározzák a szállítási, szállítási vagy logisztikai költségek. A raktár helyének meghatározására szolgáló modellekben a célfunkció minimalizálható.
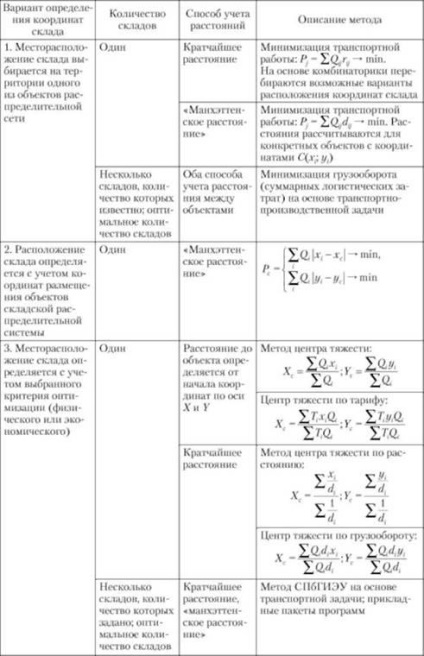
A logisztikai rendszerekben a raktár helyének meghatározására szolgáló fő módszereket a táblázat tartalmazza. 7.5.
Határozza meg a raktárak számát.
A logisztika feladata - a raktárak számának meghatározása a kiszolgált régióban - sokat fizet
Táblázat 7.5. Az ellátási láncban lévő raktárak elhelyezési módszerei
A raktárak számának meghatározására vonatkozó feladat megoldásához a következő lehetőségek tekinthetők meg.
Az első lehetőség raktárak használata nélkül. Ehhez a megoldáshoz javasoljuk, hogy megoldja a klasszikus közlekedési problémát, amely a fogyasztók számára biztosítja a fogyasztókat.
A második lehetőség egy raktár. Az ebben a változatban szereplő megoldás (raktári koordináták) számszerű keresési algoritmussal határozható meg, minimálisra csökkentve a szállítási munkát.
A harmadik lehetőség két vagy több raktár. Tulajdonságai számítások szerint a harmadik kiviteli alak azzal jellemezhető, hogy egyrészt, a bemeneti feltétel a közelítő egyenlőség raktárkapacitások (ha raktári kapacitás változtatható, a probléma válik multiobjective); másodsorban az X (vagy Y) tengely mentén lévő raktárak közötti távolság nem lehet kisebb, mint egy bizonyos érték. Ha nem adja meg ezt a mesterséges korlátozása, lehetséges degenerációja általános probléma megtalálni a szükséges szállítási költségek számától függően raktárak a legjobb megoldás.
Tekintsük az iteratív algoritmust a koordináták keresésére két raktár példáján keresztül (a 7.5. Táblázat SPPGEIU módszerként jelenik meg).
Az első szakaszban vannak kiválasztva koordinátáit az első és a második tároló, a közlekedési probléma ezután megoldott (hasonlóan az első kiviteli alak meghatározása feladatok száma raktárak) jelenlétében két T szolgáltatók és a fogyasztók (raktárak).
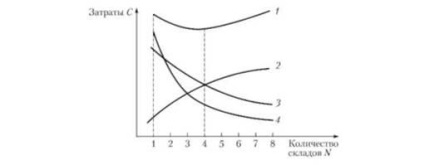
Ábra. 7.7 A komponensek függvénye és az elosztórendszer működésével kapcsolatos összes költség a raktárak számával kapcsolatban:
1 - az összes költség; 2 - a készletek tárolásának költségei, a raktárak üzemeltetése és az elosztási rendszer irányítása; 3 - az áruk szállításának teljes költsége; 4 - veszteségek a raktár távolodása miatt
A második szakaszban a szállítási feladatot ismét megoldják, de két szállító (raktár) és n fogyasztók állapota mellett.
A harmadik szakasz az első és a második szakaszban elvégzett számítások összegzése. A szállítási munka megszerzett értéke első megközelítésként kerül rögzítésre.
A negyedik szakaszban a választott szabály szerint a raktárak koordinátái megváltoznak, és az elsőtől a harmadikig terjedő számítások megismétlődnek. A raktári koordináták változatainak lekérdezése akkor fejeződik be, ha a két egymást követő iteráció szállítási műveleteinek értékei közötti különbség kisebb lesz, mint a megadott érték.
A javasolt algoritmus után kiszámíthatja a teljes logisztikai költségek szállítási összetevőjét az elosztórendszerekben két raktárral. Ez az algoritmus átalakítható olyan helyzetben, ahol több mint két raktár van a logisztikai rendszerben. Ugyanakkor a szállítási feladatot kétszer is megoldják - először a beszállítóktól a raktárakig, majd a raktáraktól a fogyasztókig.
Az 1. ábrán. A 7.8. Ábrán látható a szállítási költségek kiszámításának algoritmusa, amely a raktárak számának és helyének meghatározására szolgál.

Ábra. 7.8.Agoritmus a szállítási költségek meghatározására egy elosztóhálózatban különböző raktárak számára
Nézzük részletesebben az algoritmus lépéseit.
A probléma megoldása a fogyasztók optimális rögzítéséhez a közvetlen szállítású homogén termékek szállítói számára. Ha a beszállítók és a fogyasztók elhelyezkedését a helyük koordinátáival adják meg, akkor a szállítók és a fogyasztók km közötti legrövidebb távolságokat a (7.1) képlet határozza meg.
Az objektív funkció (a P, m-km szállítási munka minimális értéke) a következő formában írható:
ahol i = 1, m - szállító ;; = 1, n - fogyasztók; - a / szállítótól a 7. fogyasztóhoz szállított áruk mennyisége; IV. - a 7. szállító és a 7. fogyasztó súlyrészeinek terméke. Bevezetésével ez a komponens által diktált kell figyelembe venni egyéb tényezőket, amelyek befolyásolják az optimális terv biztosítására fogyasztók a szolgáltatók, például a lehetetlen közvetlen tranzitszállítmányokra / a j-edik szolgáltató th felhasználó vagy a prioritás az első fogyasztói másokkal kapcsolatban.
A teljes szállítási költség 5 kiszámítása a képlet segítségével történik
- az első szállítótól a fogyasztóig töltött lovasok száma; C0 a szállítás díja, cu / km.
Az X-ra rakott lovasok száma az alábbiak szerint kerül kiszámításra:
ahol цУ) a szállítótól a vevőig szállított járművek névleges teherbírása; t; y "a gördülőállomány felhasználási tényezője, amelyet a szállítótól a vevőig szállítanak.
A raktár helyzetének megoldása. Az ebben a fázisban használt objektív függvény:
ahol bp b-, azaz a raktártól az i. szállítóig és az y-edik fogyasztóig terjedő távolság; Körülbelül - ennek megfelelően a rakomány mennyisége egy raktáron az első szállítótól és egy raktártól a ^ - fogyasztóig.
A távolság a raktárból az / -edik vagy v-edik felhasználó által megadott (7.1), ahol X = HRW = yn - a kívánt koordinátákat a raktár, ahol a minimális a célfüggvény (7.6).
A szállítási költségeket a következő képlet segítségével számítják ki
ahol 2.p 2. - az első szállítótól a raktárig és a raktártól a fogyasztóig terjedő lovasok száma.
A raktárak koordinátáinak meghatározása a "súlypont" -hoz képest. A "súlypont" "X" és "Y" raktár koordinátáit elfogadják, és megállapítják a raktárak koordinátáinak a "súlypontra" vonatkozó szabályait. A raktáraktól a "súlypontig" való távolság meghatározásához a sorrendben végrehajtott szabályokat kell beírni:
• határozza meg a legtávolabbi egymás közötti koordináták közötti távolságot:
Ahol ХрЗД - a szállító koordinátái; ., y> a fogyasztók koordinátái;
• válassza ki a minimális távolságot és határozza meg a 7. kör sugarát, amelyen a raktárak átlósan helyezkednek el:
• a raktárakat először vízszintesen helyezik el, majd függőlegesen a koordináta tengelyekhez képest;
• az eredetileg elfogadott R = 0,1 sugár 0,2-re, majd 0,3-ra, és így tovább.
4. lépés: A raktárak különböző helyszíneinek szállítási minimális költségének kiszámítása. Két vagy több raktár jelenlétében az objektív funkció a következő formában van:
ahol r = 1, m - szállító; k = 1, / - raktárak,> = 1, n - fogyasztók; £ d, bm, ill. Az i. Szállítótól való távolság raktár és a a fogyasztó raktára; 0 ^ - - vagyis az 1. szállítótól származó áruk szállítási mennyisége raktár és a a fogyasztó raktára; AND ^ és ^ - - vagy az első beszállító és az A-es raktár, a k-es raktár és a fogyasztó súlyrészeinek terméke.
Az első szállítótól a k-es raktárig és a raktártól az i fogyasztóig terjedő távolságokat a (7.1) képlet adja meg.
A teljes szállítási költség kiszámítása az alábbi képlet szerint történik
ahol 2 [k, 2 m - vagyis az első beszállítótól a raktár raktáránál és a kettős fogyasztó raktáránál töltött lovasok száma.
A betöltött lovasok számát a (7.5) képlet alapján számítjuk ki.