"Geometria világa" lecke
"Geometria világa" lecke.
"A geometria a legerősebb eszköz
szellemi karaink finomítása és
lehetőséget ad a gondolkodásra és az indokolásra. "
Oktatás - a diákoknak a geometria szépségének bemutatása, a geometria eredetének megismerése, az alapvető geometriai fogalmak rendszerezése.
Javítás - fejlesztés - a diákok kreatív és szellemi tevékenységének fejlesztése, szellemi tulajdonságok, általánosíthatóság, gyors átállás; elősegíti a független munkatapasztalatok kialakulását; képessé teszik arra, hogy világosan és világosan megfogalmazzák gondolataikat.
Oktatási - a diákok számára a témában való érdeklődést; képesek arra, hogy pontosan és helyesen végezzenek matematikai feljegyzéseket.
Berendezés: multimédia, geometriai formák készítése, keresztrejtvény.
A lecke típusa: játék - utazás.
2. A kérdések megfogalmazása:
- Mit jelent a "geometria" szó?
- Mit tanul a geometria?
- Mikor és hogyan jött létre a tudomány "geometriája"?
- Miért kell ismerni a geometriát?
3. A téma vizsgálata:
1. Történelmi állomás.
2. Geometriai állomás.
Gyakorlati állomás.
4. Illúziós állomás.
4. Házi feladat.
5. A lecke eredményei. Reflection.
Srácok, ma már az első tanításunk egy új tudományos tárgy - geometria tanulmányozásában. Megpróbálom megmutatni a geometria szépségét, megismerni a geometria eredetének történetét, rendszerezni az Ön számára ismert alapvető geometriai fogalmakat.
Tehát elkezdjük az utazást a geometria világába (2. dia).
A notebookokban megírjuk a "A geometria világa" című leckét.
A 20. század elején a nagy francia építész, Le Corbusier elmondta (3. dia):
"Úgy gondolom, hogy ilyen geometriai időszakban soha nem éltünk a jelenben. Minden geometria.
Ezeket a szavakat nagyon pontosan jellemzi időnk. Időnk tele van a házak, utcák, hegyek és mezők geometriájával, a természet és az ember alkotásával.
Jobb, ha navigálsz ebben a világban, felfedezhetsz új és ismeretlen számot a geometriai segítségért.
Görög nyelven a "geometria" szó "földmérést" jelent ("geo" földet jelent, a "metreo" pedig "intézkedés").
Wilhelm Leibniz azt mondta: "Bárki, aki a múltra való ismeret nélkül korlátozni akarja a jelenetét, soha nem fogja megérteni."
Nézzük meg a múltat, amikor a geometria tudománya született ...
Honnan jött az új tudomány?
Ki találta fel? Adtad a nevet?
És miért kényszerített minket?
A geometria az egyik legősibb tudomány. Az első geometriai tényeket a babiloni erszényes táblákban és az egyiptomi papyriban (III. Millennium BC), valamint más forrásokban találták meg.
A geometria az emberek gyakorlati tevékenységének eredményeképpen jött létre: házakat, templomokat, utakat, öntözési csatornákat kellett építeni, földterületeket határoztunk meg és meghatároztuk a méretüket. Fontos szerepet játszottak az emberek esztétikai igényei: az otthonok és ruhák díszítésének vágya, a környező élet képeinek rajzolása.
A tudást még nem rendszerezték és nemzedékről generációra adták át, szabályok és előírások formájában.
Például a számok, a testtömegek, a derékszögek felépítése stb. Ezeknek a szabályoknak nincs bizonyítéka, és bemutatásuk nem tudományos elmélet volt.
Több évszázadon keresztül Krisztus előtt Egyiptomban, Kínában, Babilonban, Görögországban már létezett kezdeti geometriai tudás, amelyet elsősorban kísérleti eszközökkel nyertek ki, majd rendszereztek.
Az első, aki új geometriai tényeket kapott az érvelés (bizonyíték) segítségével, az ókori görög matematikus Thales (ie 6. század).
Így a geometria az emberek gyakorlati aktivitásán alapult, és önálló tudományként alakult ki, amely számokat tanulmányoz.
A geometria minden későbbi fejlődésére a legnagyobb hatást a görög Euclid tudós munkái szolgálták. aki Alexandriában élt a Kr. e. III. században.
Euklid a "The Beginnings" című esszéjét írta, és csaknem két évezredig tanulmányozta a geometriát e könyvből, és a tudós tiszteletére vonatkozó tudományt euklideszi geometriának nevezték.
Tehát a geometria olyan tudomány, amely a geometriai alakok tanulmányozásával foglalkozik.
Srácok, milyen geometriai alakzatok vannak és én már ismerem? (hallgatói válaszok). Mielőtt geometrikus formák lennének. Néhányat ismersz, és néhányat még nem tanulmányozták. Azt javaslom, hogy ezeket az adatokat két csoportba osztja (független munka). Indokolja meg, hogy ezek az elvek milyen csoportokra oszthatók (diákok válaszolnak).
Az iskolai tanfolyam két részre oszlik: planimetria és sztereometria. A planimetria síkra, sztereometriai ábrázolásra vonatkozik - a térben. Megkezdjük a geometriát a planimetriával.
A planimetria alapkoncepciói pont és sor.
A matematika tanfolyamról, amelyről tudod, (14-es dia), hogy a pontokat nagybetűs latin betűkkel jelöltük (15-ös csúszda) egyenes vonalakat - egy tőkét vagy két nagybetűs betűt.
Kiderül, hogy a pontok és a vonalak között határozott kapcsolat van.
Vegyünk egy vonalat m egy vonalat és egy A pontot. Ebben az esetben mondja: az A pont az m vonalhoz tartozik (jegyzetet a noteszgépbe). Most vegye figyelembe a B pontot, amely nem a m vonalán fekszik. Ebben az esetben mondja, hogy a B pont nem tartozik az m vonalhoz (jegyzetet a noteszgépbe).
És most ellenőrizze magát. A tartozék szimbólum használatával jegyezze fel az egyenes pontjának kapcsolódását vagy megtagadását (önálló munka az elülső ellenőrzéssel).
Kérdés: Hány egyenes vonal húzható meg két ponton keresztül? (hallgatói válaszok)
Ne feledje: bármelyik két ponton egy egyenes vonalat húzhat, és csak egy.
Kérdés: Hány egyenes vonalat lehet húzni egy ponton keresztül? (hallgatói válaszok)
Ne feledje: egy ponton rengeteg egyenes vonalat rajzolhat meg.
Ha ebből a sorból csak két sort veszünk fel, akkor ezeket a vonalakat keresztezük és a megfelelő kifejezést a noteszgépbe a kereszteződés szimbólumával írjuk (jegyezzük fel a noteszgépbe).
Srácok, a geometria segít megtalálni az érdekes kérdésekre adott válaszokat. Például a szegmensek egyenlőek? (dia 20) Mindig lehet bízni a látomásodban?
A geometria világába utaztunk. Otthon, meg kell oldanod a keresztrejtvényt.
A lecke eredménye. Reflection.
Keresztrejtvény "Kezdeti geometriai fogalmak"
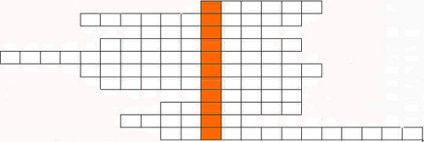
1. Helyezze be a kimaradt szót: "Minden két ponton keresztül tarthat ... és csak egy."
2. Matematikai jel 7. Matematikai jel